Anwendungsaufgaben zu den quadratischen Gleichungen
Es muss gelten:x = 10
Wir setzen den berechneten Wert bei den beiden Katheten für x ein und erhalten so ihre jeweilige Länge:
Länge der Hypotenuse in cm:
x = 10
Länge der ersten (längeren) Kathete in cm: x – 2 = 10 – 2 = 8
Länge der zweiten (kürzeren) Kathete in cm: x – 4 = 10 – 4 = 6
Nun haben wir alle drei Seiten des rechtwinkligen Dreiecks berechnet:Die Hypotenuse ist 10 cm lang, die längere Kathete 8 cm und die kürzere Kathete 6 cm. Man erkennt auf einen Blick, dass die längere Kathete um 2 cm kürzer ist als die Hypotenuse, und dass die kürzere Kathete wiederum um 2 cm kürzer ist als die längere Kathete. Die Bedingungen, die in der Aufgabe vorgegeben waren, sind also wirklich erfüllt.
Vielleicht hast du dir oben gedacht:„Dass x größer als 4 sein muss, hätte ich total übersehen! Ich hätte bestimmt gedacht, dass es hier zwei mögliche Lösungen gibt.“ Wenn du dann aber weitergerechnet hättest mit deinen beiden Werten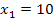 
und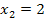 
, wärst du sicher auch darauf gekommen, dass 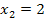keine Lösung sein kann, denn du hättest für die kürzere Kathete eine negative Länge, nämlich x – 4 = 2 – 4 = – 2, erhalten. Dass eine Länge nicht negativ sein kann, weißt du auf jeden Fall. So hättest du letztendlich doch noch gemerkt, dass es hier nur eine Lösung gibt. Gefährlich wäre es allerdings geworden, wenn nur die Hypotenuse in der Aufgabe gefragt gewesen wäre und du die Bedingungen nicht kontrolliert hättest. Daher gilt bei solchen Aufgaben die Regel:Immer noch einmal am Schluss nachrechnen, ob alle Bedingungen durch die berechneten Werte erfüllt werden!
Und nun zu den typischen Zahlenrätseln, die in so ziemlich keinem Lehrbuch fehlen. Also schauen auch wir uns ein paar typische Beispiele dafür an. Es gibt diese Art von Aufgaben in den verschiedensten Variationen. Ein richtiges Patentrezept, nach der sich jede lösen lässt, gibt es dabei leider nicht. Generell lässt sich nur sagen, dass man versucht eine Gleichung aufzustellen, die nur eine Unbekannte enthält, auch wenn eigentlich zwei Zahlen gesucht werden. In der Aufgabenstellung ist immer ein Zusammenhang dieser beiden Zahlen gegeben, so dass sich die eine Zahl immer irgendwie durch die andere ausdrücken lässt. (Die eine gesuchte Zahl nennen wir x. Wenn nun beispielsweise die andere gesuchte Zahl um 3 größer ist als die erste, kann man die zweite als x + 3 schreiben. Dann muss noch irgendein weiterer Zusammenhang zwischen den beiden Zahlen gegeben sein, z.B. ihr Produkt ist gleich 130. Mit diesen Informationen lässt sich dann die Gleichung x(x + 3) = 130 aufstellen und nach x auflösen.) Alternativ zu diesem Weg kann man manchmal auch gut mit zwei Unbekannten x und y arbeiten, für die man dann allerdings zwei Gleichungen aufstellen muss. Wichtig ist außerdem, dass du dir vorab darüber Gedanken machst, welche Werte für x überhaupt zulässig sind. Oft ist x beispielsweise eine Länge, dann muss x positiv sein. Am besten wir schauen uns das an den folgenden konkreten Beispielen genauer an.
