Anwendungsaufgaben zu den quadratischen Gleichungen

Zur Erinnerung:Die Hypotenuse ist im rechtwinkligen Dreieck immer die Seite, die gegenüber des rechten Winkels liegt. Die beiden Katheten bilden die Schenkel des rechten Winkels. Daher ist die Hypotenuse immer die längste Seite eines rechtwinkligen Dreiecks. Im rechtwinkligen Dreieck gilt der Satz von Pythagoras .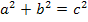

Die Länge der noch unbekannten Hypotenuse nennen wir ´mal wieder x. Die erste Kathete soll um 2 kürzer sein als die Hypotenuse;daher ist die Länge der ersten Kathete dann x – 2. Die zweite Kathete ist noch einmal um 2 kürzer als die erste Kathete. Somit kann die Länge der zweiten Kathete als x – 2 – 2 = x – 4 geschrieben werden.

Hier noch einmal alles schön übersichtlich zusammengefasst:

Länge der Hypotenuse in cm: x

Länge der ersten (längeren) Kathete in cm: x – 2

Länge der zweiten (kürzeren) Kathete in cm: x – 4

Laut Satz des Pythagoras gilt im rechtwinkligen Dreieck, dass die Summe der Kathetenquadrate gleich dem Hypotenusenquadrat ist:

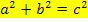(wobei a und b für die beiden Katheten und c für die Hypotenuse steht).

Wenn wir festlegen, dass a hier die längere Kathete darstellen soll und b die kürzere, dann gilt:

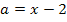
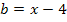
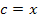
Wir setzen diese Angaben in die Formel 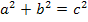ein und erhalten die folgende Gleichung:

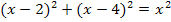
Jetzt müssen wir diese Gleichung nur noch vereinfachen und nach x auflösen.

Hinweis:Um die Klammern zu quadrieren, verwenden wir die zweite Binomische Formel .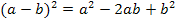

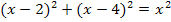
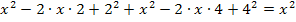
(Diesen Zwischenschritt kannst du auch weglassen und direkt die nächste Zeile aufschreiben, wenn du selbst rechnest. Der Zwischenschritt wurde speziell für diejenigen Schüler gezeigt, die Schwierigkeiten im Umgang mit den binomischen Formeln haben)

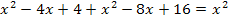
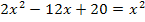
Da es sich hierbei um eine gemischtquadratische Gleichung handelt, lösen wir noch nach Null auf, damit sich danach die Mitternachtsformel anwenden lässt.

|

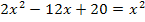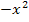
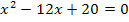
Jetzt muss man nur noch in die Mitternachtsformel einsetzen. Es gilt:a = 1 , b = -12 , c = 20

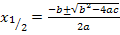
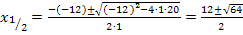
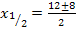
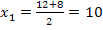
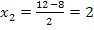
So, nun stehen wir vor dem Problem, dass wir nicht wissen, welcher dieser beiden Werte von x die gesuchte Länge der Hypotenuse darstellt. Leider sind beide Ergebnisse positiv und könnten für eine Länge somit in Frage kommen. Es gilt dabei zu beachten, dass x nicht nur positiv, sondern außerdem noch größer als 4 sein muss, denn sonst würde sich für die Länge der kürzeren Kathete x – 4 etwas Negatives (oder Null) ergeben. Damit kommt 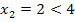nicht mehr als Lösung in Frage.

---