Anwendungsaufgaben zu den quadratischen Gleichungen
Wir nennen die Länge der kürzeren Seite des Rechtecks x. Die längere Seite ist dann x + 4, da bekannt ist, dass sie um 4 länger ist als die kürzere. (Man hätte genauso gut, die längere Seite mit x bezeichnen können. Man muss sich nur festlegen, was x sein soll. Wäre x die längere der beiden Seiten gewesen, hätte sich für die kürzere Seite eben x – 4 ergeben. Auch dieser Ansatz führt zum richtigen Ergebnis. Wir bleiben aber jetzt dabei, dass x die kürzere Seite und somit x + 4 die längere Seite ist.) Der Flächeninhalt A des Rechtecks soll gleich 165 sein. Wir ermitteln den Flächeninhalt A erst einmal in Abhängigkeit von x, damit wir diesen Term später gleich 165 setzen können. So stellen wir eine Gleichung auf, die als einzige Unbekannte die kürzere Seite x enthält. Der Flächeninhalt eines Rechtecks berechnet sich bekanntlich mit der Formel Länge mal Breite, also in unserem Fall: A =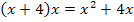 
Diesen Term setzen wir jetzt gleich 165.
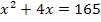
Nun liegt eine gemischtquadratische Gleichung vor. Wir lösen sie einfach mit der Mitternachtsformel. Vorher müssen wir aber noch nach Null auflösen, damit wir erkennen können, was a, b und c ist.
| 
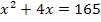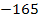
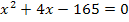
So erkennt man leicht: a = 1 , b = 4 , c = -165
Wir müssen nur noch in die Mitternachtsformel einsetzen und können x schon berechnen.
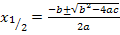
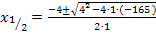
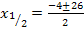
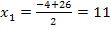
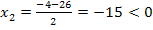
Da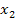 
negativ ist, kann nur 
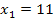die gesuchte kürzere Seite sein. (Eine Seitenlänge muss ja schließlich positiv sein.) Somit ist die kürzere Seite x = 11 und die längere Seite x + 4 = 15. Nun nehmen wir die Einheiten wieder hinzu. Die kürzere Seite des Rechtecks muss demnach 11 cm und die längere Seite 15 cm lang sein.
Zur Sicherheit kontrollierst du bei solchen Aufgaben am Ende immer noch schnell, ob die ursprünglichen Vorgaben wirklich erfüllt sind.
Hier sollten sich die beiden Seiten des Rechtecks um 4 cm unterscheiden und der Flächeninhalt sollte 165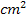 
ergeben. Dass sich 11 cm und 15 cm um 4 cm unterscheiden, sieht man sofort;den Flächeninhalt rechnen wir besser noch kurz mit dem Taschenrechner nach: 
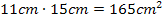Passt auch! Prima, dann sind wir wirklich fertig mit dieser Aufgabe.
Und gleich noch ein Beispiel aus der Geometrie, dieses Mal mit einem rechtwinkligen Dreieck. Für diese Aufgabe brauchen wir wieder den Satz von Pythagoras. Falls du ihn noch nicht im Unterricht gelernt hast, überspringst du das folgende Beispiel wieder und gehst direkt zum 5. Beispiel.
4. Bsp.:
In einem rechtwinkligen Dreieck ist die eine Kathete um 2 cm kürzer als die Hypotenuse und die andere Kathete wiederum um 2 cm kürzer als die erste Kathete. Berechne alle drei Seiten des Dreiecks!
Lösung:
Irgendwie klingt diese Aufgabe verdächtig einfach, aber so einfach, wie sie sich anhört, ist sie gar nicht. Mit Raten werden wir (und sollen wir ja auch gar nicht) zur Lösung kommen. Also dann müssen wir eben doch rechnen! Die Einheit cm lassen wir im Folgenden zur Vereinfachung weg.
