Anwendungsaufgaben zu den quadratischen Gleichungen
(Wie lang du a in deiner Skizze wählst ist egal, praktisch ist es beispielsweise das Dreieck mit a = 2,5 cm oder a = 3 cm zu zeichnen, dann ist es nicht zu klein und nicht zu groß. Das ist natürlich nicht der tatsächlich richtige Wert von a, den müssen wir ja letztendlich ausrechnen! Es geht hier wirklich nur darum eine Zeichnung zu machen, welche dir die Vorstellung erleichtert, denn oben ist ja nur ein Schrägbild dargestellt und dort ist nun ´mal alles verzerrt.)
So könnte deine Skizze des Dreiecks aussehen:
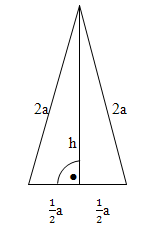
Damit wir die Dreiecksfläche in Abhängigkeit von a berechnen können, brauchen wir zuerst noch die Höhe h des Dreiecks. Wir können sie in Abhängigkeit von a folgendermaßen ermitteln:Da das Dreieck gleichschenklig ist, wird es durch die Höhe h in zwei kongruente (= deckungsgleiche) rechtwinklige Teildreiecke zerlegt. In den rechtwinkligen Teildreiecken gilt dann der Satz von Pythagoras.
Zur Wiederholung:Laut Satz des Pythagoras gilt in jedem rechtwinkligen Dreieck ABC mit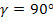 
der Zusammenhang 
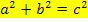(wobei a und b für die beiden Katheten und c für die Hypotenuse steht).
Mit Hilfe des Satzes von Pythagoras lässt sich nun die Höhe h in Abhängigkeit von a berechnen. Achte dabei darauf, dass der Pythagoras nur in einem der Teildreiecke angewendet werden darf, jedoch nicht im gesamten gleichschenkligen Dreieck! Der Pythagoras gilt nur in rechtwinkligen Dreiecken, aber das gesamte Dreieck ist nicht rechtwinklig. Nur die Teildreiecke sind wirklich rechtwinklig, da eine Höhe immer im rechten Winkel zu ihrer Grundlinie verläuft. Die Katheten sind hier h und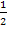 
a, da sie die Schenkel des rechten Winkels bilden. Die Hypotenuse, d.h. die Seite gegenüber des rechten Winkels, ist hier 2a. Somit gilt:
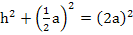Vorsicht:Klammern nicht vergessen!
| 
| 
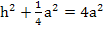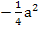
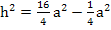
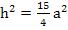
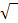
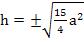
Teilweise radizieren (d.h. teilweise Wurzelziehen) ergibt dann:
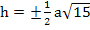
Da h eine Länge ist, kann h nicht negativ sein. Wir können deshalb die negative Lösung vergessen. Nun haben wir die Höhe h in Abhängigkeit von a dargestellt:
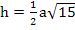
Jetzt können wir auch die Fläche eines unserer vier gleichschenkligen Dreiecke in Abhängigkeit von a berechnen. Wir wissen schließlich, dass gilt: 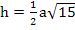und g = a
= 
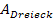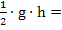
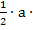
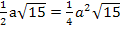
An der Außenfläche sind aber vier solche Dreiecke beteiligt, also multiplizieren wir noch mit dem Faktor 4, um die Fläche zu erhalten, welche durch die vier Dreiecke zusammen gebildet wird.
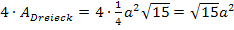
Oben haben wir schon die Fläche der vier Rechtecke in Abhängigkeit von a berechnet:
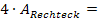
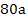
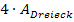und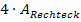 
ergeben zusammen die gesamte Außenfläche, die laut Angabe 1187,30 betragen soll:
