Anwendungsaufgaben zu den quadratischen Gleichungen
2. Bsp.:
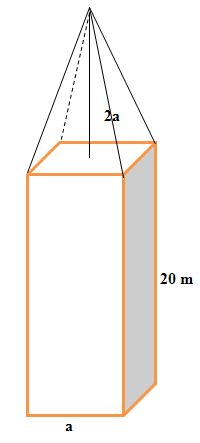
Wir sehen in der Abbildung die Skizze eines Kirchturms mit quadratischer Grundfläche. Sein Dach wird von einer vierseitigen Pyramide gebildet. Der Kirchturm besteht also aus einem Quader mit quadratischer Grundfläche, dem eine Pyramide bündig aufgesetzt wurde.
2a
Die Höhe des Quaders beträgt 20m. Die Grundfläche hat eine Länge und Breite von a Metern. Es sei außerdem bekannt, dass die vier schräg verlaufenden Kanten der Pyramide jeweils genau 2a Meter lang sind. Vergleiche Skizze! Die gesamte Außenfläche des Kirchturms (ohne Boden) beträgt 1187,30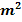 
. Ermittle a auf zwei Stellen nach dem Komma gerundet!
Lösung:
Diese Aufgabe hat es ganz schön in sich. Wahrscheinlich weißt du momentan gar nicht, wie du überhaupt beginnen sollst. Versuchen wir uns also schrittweise der Lösung zu nähern. Dem Text ist zu entnehmen, dass die gesamte Außenfläche (ohne Boden) 1187,30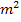 
beträgt. Da wir diese Angabe sicher irgendwie in unsere Rechnung einbeziehen müssen, überlegen wir uns zuerst, aus welchen Einzelflächen sich diese Außenfläche zusammensetzt:Der Quader steuert dabei vier gleich große Rechtecke bei und die Pyramide vier gleich große Dreiecke. Die vier Rechtecke und die vier Dreiecke sind nur deshalb jeweils gleich groß, weil die Grundfläche ein Quadrat ist. Die Höhe des Quaders kennen wir schon;sie beträgt laut Angabe 20 Meter. (Die Einheiten werden wir der Einfachheit halber in unserer Rechnung ab sofort weglassen.) Die Höhe des Quaders entspricht der Länge jeweils eines der Rechtecke. Die Breite von einem dieser Rechtecke ist jeweils a. Diese Breite a sollen wir letztendlich berechnen. Wir müssen daher eine Gleichung aufstellen, die als einzige Unbekannte a enthält. Daher rechnen wir in Abhängigkeit von a, d.h. wir rechnen mit a so, als wenn wir a schon wüssten, setzen aber für a natürlich keine konkrete Zahl ein. Die Fläche eines dieser Rechtecke ist dann wegen Länge mal Breite 
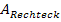= 20a und somit die Fläche aller vier Rechtecke zusammen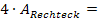 
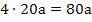. Soweit dürfte noch alles klar sein.
Nun zu den Dreiecken, die von der Pyramide beigesteuert werden:Die Fläche eines Dreiecks berechnet sich bekanntlich mit der Formel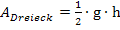 
(wobei g für Grundlinie und h für die Höhe des Dreiecks steht) Die Grundlinie eines dieser Dreiecke ist in unserem Fall a. Die Höhe kennen wir leider nicht. Wir wissen aber aus der Angabe, dass die Pyramide Seitenkanten der Länge 2a besitzt. Unsere Dreiecke sind daher gleichschenklig, wobei die Basis die Länge a hat und die Schenkel die Länge 2a. Damit du dir das besser vorstellen kannst, machst du dir am besten eine Skizze eines solchen Dreiecks. Zeichne auch gleich die Höhe zur Grundlinie a ein!
