Anwendungsaufgaben zu den quadratischen Gleichungen
Nun wieder zurück zu unserer Aufgabe:Die Flächenmaßzahl des gesamten Rechtecks beträgt 7,5. Die Fläche der vier Quadrate gemeinsam soll 30% der Rechtecksfläche betragen. Wir müssen daher berechnen, was 30% von 7,5 ist. Das ist gar nicht schwer:Wie du weißt, bedeutet % (Prozent) nichts anderes als durch Hundert und das entspricht wiederum nichts anderem als einer Verschiebung des Kommas um zwei Stellen nach links:
30% = 0,30 = 0,3
In der Mathematik entspricht außerdem das Wörtchen „von“ immer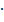 
(mal) und deshalb berechnet man 30% von 7,5, indem man einfach 0,3 mit 7,5 multipliziert.
30% von 7,5 = 0,3 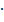7,5 = 2,25
Die Flächenmaßzahl der vier Quadrate gemeinsam soll demnach 2,25 sein. Da sich die Fläche (genau genommen wieder die Flächenmaßzahl) eines Quadrats jeweils mit x 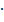x = 
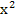und somit die aller vier Quadrate zusammen mit 4 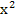berechnet, muss gelten:
4 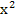= 2,25
Dies ist eine einfach zu lösende, weil reinquadratische Gleichung. (Vergleiche dazu Typ I bei Rechnerische Lösungsverfahren quadratischer Gleichungen) Wir brauchen nur noch durch 4 zu dividieren, um 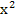zu isolieren und dann die Wurzel ziehen. Auf das Plus/Minus können wir hier direkt verzichten, denn laut Angabe gilt: 
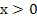Das ist ja auch logisch, denn x steht für eine Längenmaßzahl und Längen können natürlich nicht negativ sein.
4 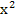= 2,25
| 
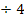
oder mit Brüchen: 4 =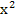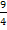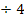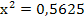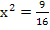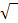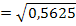 
|
| 
|
x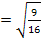 
x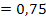 
x 
x =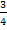 
Ob du lieber mit Dezimalzahlen und dem Taschenrechner arbeitest oder lieber im Kopf und mit Brüchen, bleibt natürlich dir überlassen. Auf jeden Fall wissen wir nun die Lösung:
x = 0,75 bzw. x =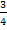
Man hätte diese Aufgabe auch mit einem Gesamtansatz lösen können. Der müsste dann so aussehen:
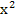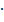4 = 0,3 3,0 2,5
Daraus ergibt sich natürlich wieder die Gleichung 4 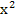= 2,25. (Das kannst du selbst ganz leicht mit dem Taschenrechner überprüfen.) Danach geht es weiter wie oben gezeigt. Noch einmal durchrechnen wollen wir das jetzt nicht mehr. Schauen wir uns lieber ein weiteres Beispiel an. Die folgende Aufgabe setzt allerdings Kenntnisse über den Satz von Pythagoras voraus. Solltest du ihn noch nicht gelernt haben, überspringst du diese Aufgabe einfach und machst direkt mit dem 4. Beispiel weiter! Aber eigentlich müsstest du den Pythagoras gerade eben gelernt haben. Die Satzgruppe des Pythagoras ist in vielen G8 Schulbüchern meist ein Kapitel vor den quadratischen Gleichungen bzw. Funktionen. Wenn du auf ein bayerisches Gymnasium gehst und gerade in der 9. Klasse bist, müsstest du somit den Pythagoras schon beherrschen. Bei Realschülern kann das allerdings anders aussehen.
