Anwendungsaufgaben zu den quadratischen Gleichungen
zu b.)
Nun zur nächsten Frage:Wie weit darf der 1,67 m hohe Zaun höchstens von der Garagenwand entfernt sein, damit Rudi ihn mit seinen Zehenspitzen bei seinem Sprung gerade nicht berührt? Wir ermitteln zuerst einmal aus, in welcher Entfernung x zum Ursprung sich Rudis Zehenspitzen während des Sprungs genau in 1,67 m Höhe befinden. Da in der Aufgabe wieder nach dem Abstand des Zaunes zur Garagenwand und nicht zum Ursprung gefragt wird, muss danach noch der Abstand des Ursprung zur Garagenwand mit 0,60 m berücksichtigt und vom vorher berechneten Wert abgezogen werden.
Doch wie berechnet man denn nun den Wert von x, bei dem sich Rudis Zehenspitzen in 1,67 m Höhe über dem Boden befinden? Ganz einfach:Der Funktionswert h(x) der gegebenen Parabel h(x) =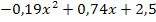 
steht ja genau für die Höhe (in Metern), in der sich seine Zehenspitzen im Abstand x zum Ursprung befinden. Wir kennen also die y-Koordinate – die ist natürlich y = 1,67 – und suchen die entsprechende x-Koordinate eines Punktes, der sich genau auf der Flugbahn, d.h. auf der Parabel h, befindet. (Zur Erinnerung:y und h(x) sind nur verschiedene Schreibweisen für den Funktionswert.) Es muss demnach gelten:
y = 1,67 bzw. h(x) = 1,67
Daher setzen wir nun für h(x) den Wert 1,67 in die Parabelgleichung ein. Wir erhalten dadurch die folgende gemischtquadratische Gleichung:
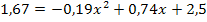
Wir bringen noch die Zahl 1,67 auf die rechte Seite der Gleichung, damit wir dann die Mitternachtsformel verwenden können.
| 
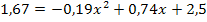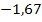
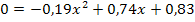
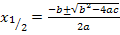
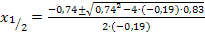
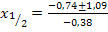
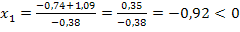
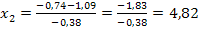
Da die gesuchte x-Koordinate positiv sein muss, kommt nur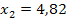 
in Frage. Der Punkt (4,82|1,67) liegt also auf der Parabel bzw. auf der Kurve, die Rudis Zehenspitzen bei dem Sprung beschreiben.
