Anwendungsaufgaben zu den quadratischen Gleichungen
a.) Rudi will auf direktem Weg in die Mitte des Pools springen. Wie weit müsste der Mittelpunkt des Swimmingpools dann von der Außenwand der Garage horizontal entfernt sein? Runde auf 2 Dezimalen!
b.) Wie weit darf der Zaun höchstens von der Garagenwand entfernt sein, damit Rudi den Zaun gerade noch überspringen kann, ohne ihn mit den Zehenspitzen zu streifen? Runde auf 2 Dezimalen!
Lösung:
Laut Angabe beschreiben Rudis Zehenspitzen eine parabelförmige Kurve mit der Gleichung h(x) =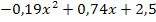 
, wobei x der horizontale Abstand seiner Zehenspitzen vom Absprungpunkt A ist und h(x) die Höhe, in der sich seine Zehenspitzen dort befinden. Vorsicht:x ist nicht die Entfernung von der Garagenwand, sondern vom Ursprung des Koordinatensystems;die Garagenwand ist ja 60 cm = 0,60 m weiter vorne! Der Ursprung des Koordinatensystems liegt nämlich auf Höhe des Bodens senkrecht unter Rudis Absprungpunkt A und nicht direkt bei der Garagenwand. Daher kann x nur positive Werte annehmen:x 
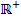Man erkennt dies auch in der Skizze:Der Graph der Funktion h(x) ist nur rechts der y-Achse gezeichnet. Rudi springt also vom Garagendach aus nach rechts zum Swimmingpool hin.
zu a.)
Die Wasseroberfläche des Swimmingpools befindet sich ebenerdig, d.h. in der Höhe h(x) = 0. Im Prinzip muss also die positive Nullstelle der Funktion h(x) berechnet werden, um herauszufinden, in welcher Entfernung x (vom Ursprung) sich Rudis Zehenspitzen bei dem Sprung auf Höhe des Bodens befinden. Damit er die Wasseroberfläche des Swimmingpools genau in der Mitte trifft, müsste dort der Mittelpunkt des Swimmingpools liegen. Der so berechnete Wert von x ist aber noch nicht die gesuchte Entfernung des Poolmittelpunks von der Garagenwand, sondern erst der Abstand des Poolmittelpunkts vom Ursprung. Um wirklich die gesuchte Entfernung des Poolmittelpunkts von der Garagenwand zu berechnen, muss noch 0,60 m vom vorher ermittelten Wert x abgezogen werden. Diese Teilaufgabe ist somit eigentlich nichts anderes als eine Nullstellenberechnung, die in einen langen Text verpackt ist. Dann muss zwar noch 0,60 m vom Ergebnis abgezogen werden;aber das ist ja kein Problem mehr. (Nur vergessen, darfst du es auch nicht!)
Wie man die Nullstelle(n) einer Funktion berechnet, weißt du:Wir müssen die Funktion einfach gleich Null setzen. Also, los geht´s!
h(x) = 0
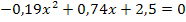
Wir wenden die Mitternachtsformel mit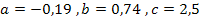 
an, um die vorliegende gemischtquadratische Gleichung nach x aufzulösen.
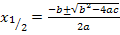
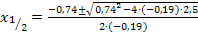
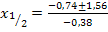
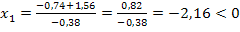
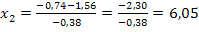
Da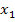 
negativ ist, fällt wegen x 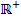dieses Ergebnis weg. Damit ergibt sich als einzige Lösung:x = 6,05
Dies bedeutet, dass Rudi in 6,05 Metern Entfernung vom Ursprung des Koordinatensystems am Boden auftreffen würde. Damit er eben nicht am Boden aufschlägt, sondern mitten in den Pool fällt, muss sich der Poolmittelpunkt genau in dieser Entfernung zum Ursprung befinden. Da die Garagenwand vom Ursprung noch 0,60 Meter weit entfernt ist, müssen wir diesen Abstand noch von 6,05 m abziehen, um den gesuchten Abstand des Poolmittelpunkts von der Garagenwand zu erhalten: 6,05 m – 0,60 m = 5,45 m
Der Swimmingpool müsste sich demnach in 5,45 m Entfernung von der Garagenwand befinden, damit Rudi bei so einem Sprung genau in die Mitte des Pools fallen würde.
