Anwendungsaufgaben zu den quadratischen Gleichungen
Beispiel:749 hat die Hunderter-Ziffer 7, die Zehner-Ziffer 4 und die Einer-Ziffer 9. Auf die Zahl 749, in Worten Siebenhundertneunundvierzig, kommt man ausgehend von ihren einzelnen Ziffern folgendermaßen:
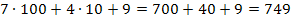
Jede einzelne Ziffer muss also noch mit ihrem Wert multipliziert werden, damit sich nach der Addition der einzelnen Faktoren wirklich die Zahl selbst ergibt.
Nun wieder zurück zu unserer Aufgabe. Wir müssen die ursprüngliche Zahl und die Spiegelzahl durch ihre Ziffern ausdrücken. Beginnen wir mit der ursprünglichen Zahl. Die Zehner-Ziffer x muss mit ihrem Wert 10 multipliziert und zur Einer-Ziffer x – 1 addiert werden. Die Zahl berechnet man demnach mit 10x + x – 1 = 11x + 1
Bei ihrer Spiegelzahl gehen wir entsprechend vor, also die Zehner-Ziffer x – 1 mit 10 multiplizieren und dazu die Einer-Ziffer x dazuzählen. Die Spiegelzahl berechnet man daher mit 10(x – 1) + x = 10x – 10 + x = 11x -10
Ursprüngliche Zahl:
Spiegelzahl:
Zehner-Ziffer : x Zehner-Ziffer : x – 1
Einer-Ziffer: x – 1 Einer-Ziffer: x
Zahl insgesamt: 10x + x – 1 = 11x – 1 Spiegelzahl insgesamt: 10(x – 1) + x =
= 10x – 10 + x = 11x -10
Der Aufgabenstellung ist zu entnehmen, dass die Zahl 11x – 1 multipliziert mit ihrer Spiegelzahl 11x – 10 genau den Wert 736 ergibt. Als Gleichung geschrieben sieht das dann folgendermaßen aus:
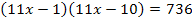
Nun haben wir endlich eine Gleichung mit der Zehner-Ziffer x (der ursprünglichen Zahl) als Unbekannte vorliegen. Wir müssen sie bloßnoch nach x auflösen, doch das dürfte inzwischen kein Problem mehr für dich darstellen. Rechne nun alleine weiter! Damit du deine Rechnung kontrollieren kannst, folgt hier der restliche Lösungsweg:
| 
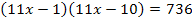
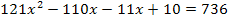
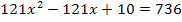
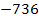
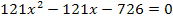
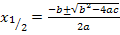
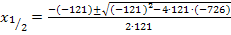
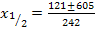
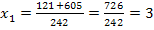
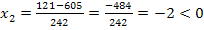
Da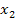 
negativ ist, fällt dieses Ergebnis weg. Damit ergibt sich als einzige Lösung x = 3. Die Zehner-Ziffer der ursprünglichen Zahl muss also 3 sein. Da die Einer-Ziffer um 1 kleiner sein soll, muss die Einer-Ziffer der ursprünglichen Zahl 2 sein. Die gesuchte Zahl ist demnach 32.
Wir überprüfen noch schnell, ob wirklich alle Bedingungen aus dem Text erfüllt sind. Dass bei der Zahl 32 die Einer-Ziffer um 1 kleiner ist als die Zehner-Ziffer, sieht man sofort. Die Spiegelzahl von 32 ist logischerweise 23. Wir bilden das Produkt der Zahl 32 und ihrer Spiegelzahl 23:
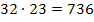
Das stimmt mit der Forderung im Text überein.
