Anwendungsaufgaben zu den quadratischen Gleichungen
Die Zehner-Ziffer der ursprünglichen Zahl nennen wir x.´(Man hätte natürlich genauso gut, die Einer-Ziffer dieser Zahl mit x bezeichnen können.)
Info:Eine Ziffer ist – im Unterschied zu einer Zahl, die auch aus mehreren Ziffern bestehen kann – immer eine einstellige natürliche Zahl oder Null. Eine Ziffer ist also eine ganze Zahl zwischen Null und Neun.
x stellt hier ja eine Ziffer dar;daher gilt:x 
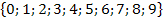Genau genommen stimmt das noch nicht ganz, denn x kann hier nicht 0 sein! Laut Angabe ist die Einer-Ziffer um 1 kleiner als die Zehner-Ziffer x. Wäre x = 0, würde sich für die Einer-Ziffer -1 ergeben und das ist schließlich keine Ziffer mehr, wegen des negativen Vorzeichens! Dass x nicht gleich 0 sein kann, merkt man auch schon daran, dass die gesuchte Zahl zweistellig sein soll. Eine Zahl mit 0 am Anfang, z.B. 03 = 3 oder 07 = 7, ist schließlich nicht zweistellig! Ganz korrekt wäre somit x 
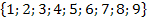
Die Einer-Ziffer der ursprünglichen Zahl ist ja laut Angabe um 1 kleiner als die Zehner-Ziffer x der selben Zahl. Die Einer-Ziffer der ursprünglichen Zahl kann daher als x – 1 geschrieben werden.
Ursprüngliche Zahl:
Zehner-Ziffer :
x
Einer-Ziffer: x – 1
Die Spiegelzahl erhält man, indem man die beiden Ziffern vertauscht.
Spiegelzahl:
Zehner-Ziffer : x – 1
Einer-Ziffer: x
Soweit dürfte noch alles klar sein. Doch jetzt kommt der entscheidende Schritt:Wir müssen die ursprünglichen Zahl (insgesamt) und die Spiegelzahl (insgesamt) jeweils in Abhängigkeit von x ermitteln, damit wir letztendlich die ursprüngliche Zahl mit ihrer Spiegelzahl multiplizieren können. Wir wissen ja, dass dieses Produkt 736 ergeben soll.
Um eine zweistellige Zahl aus ihren einzelnen Ziffern zu berechnen, muss die Zehner-Ziffer der Zahl mit ihrem Wert 10 multipliziert und die Einer-Ziffer dazu addiert werden.
Mache dir diese Aussage am besten an irgendeinem konkreten Beispiel klar. Nehmen wir beispielweise die Zahl 62. (Das hat gerade nichts mit unserer gesuchten Zahl zu tun;62 ist nur ein beliebig gewähltes Zahlenbeispiel.) Die Zehner-Ziffer ist hier 6 und die Einer-Ziffer ist 2. Will man aus diesen einzelnen Ziffern wieder auf die Zahl 62 (in Worten Zweiundsechzig) kommen, muss man die Zehner-Ziffer 6 zuerst mit 10 multiplizieren und dann die Einer-Ziffer 2 dazu addieren:
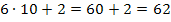
Entsprechend müsste man bei einer dreistelligen Zahl vorgehen:Hunderter-Ziffer mit 100 multiplizieren, Zehner-Ziffer mit 10 multiplizieren, dann diese beiden Ergebnisse und die Einer-Ziffer addieren.
