Anwendungsaufgaben zu den quadratischen Gleichungen
Wir müssen diese Information jetzt nutzen, um zu unserer Gleichung zu kommen. Weil 4x um 1 kleiner ist als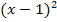 
, muss zu 4x die Zahl 1 addiert werden, damit man 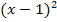erhält. Die Gleichung muss daher lauten:
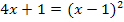
Vielen Schüler macht dieser Schritt erfahrungsgemäßSchwierigkeiten. Oft kommt an dieser Stelle die Frage, warum man denn zu 4x die Zahl 1 addiert und nicht subtrahiert. Wenn auch dir dies nicht klar ist, überlege dir folgendes:Der Ausdruck 4x ist kleiner (nämlich um 1) als der Ausdruck 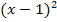. Willst du eine Beziehung mit Gleichheitszeichen in der Mitte, also eine Gleichung, aufstellen, musst du zu dem Kleineren etwas dazu zählen, damit es genauso großwird wie das Größere. Das ist der Grund, warum man zu dem kleineren 4x die Zahl 1 dazu zählen muss, damit man das um 1 größere 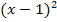bekommt. Man hätte natürlich auch von dem größeren 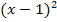die Zahl 1 abziehen können, um das kleinere 4x zu erhalten. Die Gleichung 
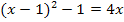ist demnach natürlich ebenfalls richtig.
Jetzt müssen wir nur noch nach x auflösen. Dazu vereinfachen wir die Gleichung so weit möglich, d.h. wir rechnen die Klammer mit der zweiten Binomischen Formel aus, bringen alles auf eine Seite der Gleichung und fassen zusammen. Die Mitternachtsformel brauchen wir hier nicht unbedingt, obwohl es sich hier um eine gemischtquadratische Gleichung handelt. Du wirst gleich sehen, warum. Ab jetzt kommt also der angenehmere Teil der Aufgabe. Das schaffst du bestimmt alleine! Zur deiner Kontrolle kommt jetzt natürlich auch noch der Rest der Rechnung:
| 
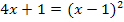
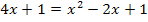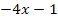
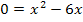
Da bei dieser gemischtquadratischen Gleichung die Konstante c fehlt (c = 0), können wir x einfach ausklammern. Dadurch entsteht ein Produkt und ein Produkt ist bekanntlich gleich Null, wenn einer der Faktoren gleich Null ist. Deshalb setzen wir einfach die einzelnen Faktoren, als x und die Klammer, jeweils einzeln gleich Null. Vergleiche dazu auch Typ II bei Rechnerische Lösungsverfahren quadratischer Gleichungen!
, 
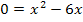
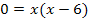
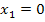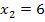
Da für die gesuchte Zahl gelten muss x 
ℕ kommt die Null nicht in Frage. Die Zahl muss 6 sein. Wir kontrollieren noch einmal die Bedingung, dass das Vierfache der Zahl, also hier 24, um 1 kleiner sein soll als das Quadrat der um 1 verringerten Zahl. Die Zahl 6 um 1 verringert ist natürlich 5, das Quadrat von 5 ist logischerweise 25. Das Vierfache der Zahl, also 24, ist um 1 kleiner als 25. Also passt alles! Fertig!
Lösung zu d.)
Hier noch einmal die Angabe:
Die Einer-Ziffer einer zweistelligen Zahl ist um 1 kleiner als die Zehner-Ziffer dieser Zahl. Multipliziert man diese Zahl mit ihrer Spiegelzahl ergibt sich 736. Was war die ursprüngliche Zahl? (Die Spiegelzahl erhält man durch Vertauschen der Einer- und Zehner-Ziffer.)
So, diese Aufgabe ist wirklich nicht einfach.
