Anwendungsaufgaben zu den quadratischen Gleichungen
Wir bilden zuerst auf der linken Seite den Hauptnenner der beiden Brüche, damit wir danach kreuzweise multiplizieren können. (Anmerkung:Man hätte auch mit dem Hauptnenner der gesamten Gleichung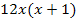 
auf beiden Seiten multiplizieren können. Genaueres dazu im Kapitel Bruchgleichungen.) Wir wollen jedoch die beiden Brüche auf der linken Seite der Gleichung auf einen gemeinsamen Nenner bringen. Der Hauptnenner der beiden Brüche 
und 
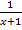ist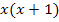 
. Um sie auf den Hauptnenner zu bringen, muss der erste Bruch mit x+1 und der zweite Bruch mit x erweitert werden.
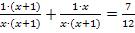
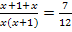
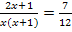
Nun kann kreuzweise multipliziert werden.
| 
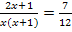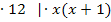
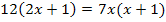
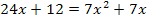
Nun erkennt man, dass wieder eine gemischtquadratische Gleichung vorliegt. Wie man sie nach x auflöst, müsste dir inzwischen klar sein.
| 
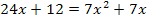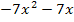
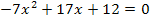
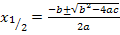
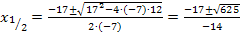
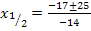
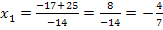
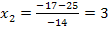
Das erste Ergebnis ist keine natürliche Zahl;somit kommt als Lösung nur x = 3 in Frage. Die kleinere Zahl müsste also 3 sein. Der Nachfolger von 3 ist natürlich die Zahl 4. Wir kontrollieren noch einmal, ob die Forderung, dass die Summe der Kehrwerte dieser beiden Zahlen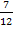 
ergibt, erfüllt ist.
Der Kehrwert von 3 ist 
. Der Kehrwert von 4 ist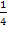 
. Die Summe der beiden Kehrwerte berechnen wir noch schnell:
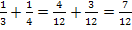
Stimmt! Also sind die gesuchten Zahlen 3 und 4.
Lösung zu c.)
Hier noch einmal die Angabe:
Das Vierfache einer Zahl ist um 1 kleiner als das Quadrat der um 1 verringerten Zahl. Wie lautet die Zahl?
Diese Aufgabe ist nicht schwer, versuche sie doch erst einmal alleine, bevor du dir die Lösung anschaust! Hier gibt es auch nur einen möglichen Rechenweg, da nur eine Zahl gesucht ist.
Lösung:
Hier ist nur eine einzelne Zahl gesucht. Wir nennen sie wieder x. Das Vierfache der Zahl ist dann 4x. Das Vierfache der Zahl soll um 1 kleiner sein als das Quadrat der um 1 verringerten Zahl. Also muss man sich erst ´mal überlegen, was der Ausdruck „Quadrat der um 1 verringerten Zahl“ bedeutet. Von der Zahl x soll zuerst 1 abgezogen werden und das Ergebnis soll dann quadriert werden. Das Quadrat der um 1 verringerten Zahl ist somit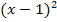 
. (Anmerkung: 
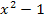wäre hier falsch, denn das würde ja bedeuten, dass zuerst quadriert und danach erst die Zahl 1 abgezogen würde!) Jetzt muss man ganz besonders aufpassen, denn beim nächsten Schritt passiert sehr leicht ein Fehler. In der Angabe steht, dass das Vierfache der Zahl, also 4x, um 1 kleiner ist als das Quadrat der um 1 verringerten Zahl, also .
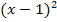