Anwendungsaufgaben zu den quadratischen Gleichungen
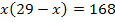
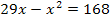
Nun erkennst du, dass es sich um eine gemischtquadratische Gleichung handelt. Wir wollen sie mit der Mitternachtsformel lösen. Daher muss vorher nach Null aufgelöst werden:
| 
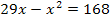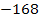
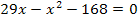
Wir ordnen noch nach absteigenden Potenzen von x.
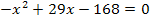
Nun kannst du gut ablesen, was a, b und c ist: a = -1 , b = 29 , c = -168
Einsetzen in die Mitternachtsformel ergibt:
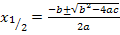
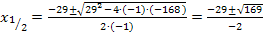
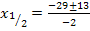
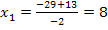
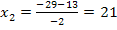
Beide Ergebnisse sind natürliche Zahlen und kommen somit als Lösungen in Frage.
Nun wunderst du, dich sicher, dass hier zwei verschiedene Lösungen heraus kommen. Das liegt daran, dass es egal ist, welches der beiden Ergebnisse man als erste Zahl x und welche man als zweite Zahl 29 – x ansieht.
Nimmt man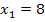 
als erste Zahl, so ergibt sich wegen 29 – 
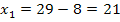für die zweite Zahl der Wert 21. Umgekehrt ergibt sich für die zweite Zahl der Wert 8, wenn man 
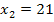als erste Zahl nimmt. Das bedeutet also die beiden gesuchten Zahlen müssen 8 und 21 sein. Zum Schluss überprüfen wir noch einmal, ob die Forderungen „Summe ist 29“ und „Produkt ergibt 168“ wirklich erfüllt sind. Dass 8 und 21 addiert 29 ergeben ist klar;bleibt noch das Produkt zu kontrollieren:
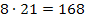
Super, das passt auch! Damit ist diese Aufgabe gelöst. Die Zahlen lauten tatsächlich 8 und 21.
Lösung zu b.)
Hier noch einmal die Angabe:
Addiert man die Kehrwerte von zwei aufeinanderfolgenden natürlichen Zahlen, so erhält man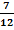 
. Wie lauten die beiden Zahlen?
Lösung:
Gesucht sind hier zwei aufeinanderfolgende natürliche Zahlen. Die kleinere der beiden nennen wir x. (x 
ℕ) Da die beiden Zahlen direkt aufeinander folgen sollen, muss die zweite um 1 größer sein als die erste Zahl. Die zweite Zahl lässt sich daher als x + 1 schreiben.
Kleinere Zahl:
x
Größere Zahl: x + 1
Kehrwert der kleineren Zahl: 
Kehrwert der größeren Zahl: 
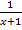
Laut Angabe soll die Summe der beiden Kehrwerte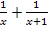 
den Wert 
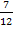ergeben. So erhält man die folgende Gleichung:
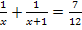
Auf diese Gleichung kommt man ebenfalls mit dem zweiten Lösungsverfahren. Wie bei Teilaufgabe 5a.) bereits beschrieben, kann man die beiden gesuchten Zahlen als x und y bezeichnet, erst ´mal zwei Gleichungen mit x und y aufstellen, dann eine der Gleichungen nach y auflösen und in die andere Gleichung einsetzen. Wenn du den anderen Lösungsweg auch sehen möchtest, gehe zu:Lösungsweg 2 zu Bsp. 5b (mit zwei Gleichungen für zwei Unbekannte)
Es handelt sich um eine Bruchgleichung, da die Unbekannte x im Nenner vorkommt.
