Anwendungsaufgaben zu den quadratischen Gleichungen
5. Bsp.:
Zahlenrätsel
a.) Die Summe zweier natürlicher Zahlen ergibt 29. Ihr Produkt ergibt 168. Wie lauten die beiden Zahlen?
b.) Addiert man die Kehrwerte von zwei aufeinanderfolgenden natürlichen Zahlen, so erhält man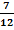 
. Wie lauten die beiden Zahlen?
c.) Das Vierfache einer Zahl ist um 1 kleiner als das Quadrat der um 1 verringerten Zahl. Wie lautet die Zahl?
d.) Die Einer-Ziffer einer zweistelligen Zahl ist um 1 kleiner als die Zehner-Ziffer dieser Zahl. Multipliziert man diese Zahl mit ihrer Spiegelzahl ergibt sich 736. Was war die ursprüngliche Zahl? (Die Spiegelzahl erhält man durch Vertauschen der Einer- und Zehner-Ziffer.)
Lösung:
zu a.)
Wir suchen hier zwei natürliche Zahlen, die addiert 29 und miteinander multipliziert168 ergeben sollen. Natürlich könntest du nun anfangen systematisch zu probieren. Wahrscheinlich würdest du die Lösung auch auf diese Art und Weise finden. Uns geht es hier jedoch weniger um das Endergebnis als vielmehr um den Rechenweg. Du willst schließlich lernen, wie man bei solchen Aufgaben prinzipiell vorgeht. Also müssen wir eine Gleichung aufstellen, in der eine unserer gesuchten Zahlen als einzige Unbekannte auftritt. Wie gewöhnlich nennen wir die eine der gesuchten Zahlen x. Da es sich laut Angabe um eine natürliche Zahl handeln soll, gilt:x 
ℕ
Die andere Zahl müssen wir nun irgendwie durch x ausdrücken, damit keine zweite Unbekannte in unserer Gleichung auftaucht. Die zweite gesuchte Zahl lässt sich in diesem Fall als 29 – x schreiben, da die beiden Zahlen addiert ja schließlich 29 ergeben sollen.
Erste Zahl: x
Zweite Zahl: 29 – x
Laut Angabe soll das Produkt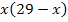 
der beiden Zahlen 168 ergeben. Mit dieser Information kann man die folgende Gleichung aufstellen:
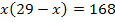
Man kann hier allerdings auch nach einem anderen Verfahren vorgehen. Es besteht nämlich auch die Möglichkeit die beiden gesuchten Zahlen x und y zu nennen. Dann müssen zwei Gleichungen für die beiden Unbekannten x und y aufgestellt werden. Die oben gezeigte Gleichung erhält man dann, indem beispielsweise eine Gleichung in die andere eingesetzt wird. Ob dir das leichter fällt, kann bezweifelt werden. Letztendlich kannst nur du selber sagen, was du leichter findest. Wenn du den anderen Lösungsweg auch sehen möchtest, gehe zu:Lösungsweg 2 zu Bsp. 5a (mit zwei Gleichungen für zwei Unbekannte)
Die benötigte Gleichung steht endlich da, also haben wir das Schlimmste jetzt hinter uns. (Das Problem der meisten Schüler ist es ja, erst ´mal auf diese Gleichung zu kommen.) Wir müssen unsere Gleichung nur noch nach x auflösen. Dazu multiplizieren wir die linke Seite erst einmal aus. Alles Weitere dürfte eigentlich kein Problem mehr darstellen. Trotzdem wird auch der Rest dieser Aufgabe noch ausführlich vorgerechnet.
