Wertemenge und Symmetrieachse

Der Scheitel ist daher der Tiefpunkt bzw. das Minimum der Funktion f. 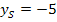ist somit der kleinstmögliche y-Wert, den die Funktion annehmen kann. Alle anderen y-Werte sind größer als 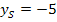. Es können also nur Zahlen für y herauskommen, die größer oder gleich -5 sind.

Die Wertemenge lautet: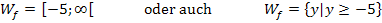

Symmetrieachse einer quadratischen Funktion ermitteln:

Um die Gleichung der Symmetrieachse einer Parabel angeben zu können, muss eigentlich nur die x-Koordinate 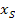des Scheitels bekannt sein. Die Symmetrieachse einer quadratischen Funktion 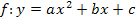ist immer eine senkrechte Gerade, die genau durch den Scheitelpunkt S verläuft. Die Symmetrieachse einer Parabel hat daher die Gleichung 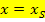. (Mehr zu senkrechten Geraden im Kapitel Waagrechte und senkrechte Geraden)

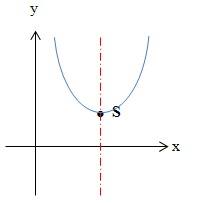
Symmetrieachse

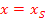
Abb.:Parabel mit Symmetrieachse (rot dargestellt)

Schauen wir uns doch gleich ´mal ein paar Beispiele an.

1. Bsp.:

Gib die Gleichung der Symmetrieachse der Funktio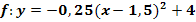n an!

Lösung:

Da die Funktion in Scheitelform gegeben ist, kann die x-Koordinate des Scheitels direkt abgelesen werden: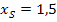

Die Gleichung der Symmetrieachse lautet: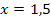

Das war schon alles!

2. Bsp.:

Gib die Gleichung der Symmetrieachse der Funktio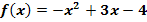n an!

Lösung:

Die Funktion liegt noch nicht in Scheitelform vor. Damit die x-Koordinate des Scheitels abgelesen werden kann, verwenden wir wieder die quadratische Ergänzung. Vergleiche Quadratische Ergänzung zur Scheitelberechnung!

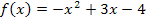
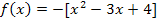
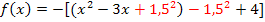
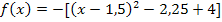
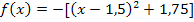
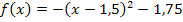
Nun liegt die Parabel in Scheitelform vor und wir können leicht die x-Koordinate des Scheitels ablesen: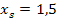

Daher lautet die Gleichung der Symmetrieachse 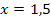. Fertig!

---