Wertemenge und Symmetrieachse

Setzt man für x sehr große Zahlen ein, wird auch y sehr groß. Man sagt:Wenn x gegen Unendlich geht, geht auch y gegen Unendlich. Das sieht man auch deutlich am Graph:Er verläuft vom Scheitel aus gesehen nach oben.

Umgekehrt ist der Scheitel das absolute Maximum der Parabel, wenn a negativ ist, da die Parabel dann nach unten geöffnet ist. Für 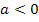ist die y-Koordinate des Scheitels also der größte y-Wert, den die Funktion 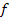annehmen kann. Alle anderen y-Werte sind kleiner als 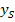. Am Graph sieht man das natürlich ebenfalls:Er verläuft vom Scheitel gesehen nach unten.

Die Wertemenge lautet daher allgemein:

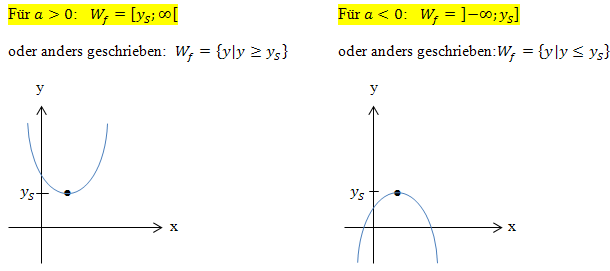
oder anders geschrieben: 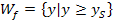oder anders geschrieben:

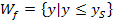
Wenn dir das alles zu theoretisch war, wird es dir hoffentlich gleich an Hand der folgenden Beispiele klar.

1. Bsp.:

Gib die Wertemenge 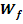der Funktio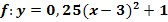n an!

Lösung:

Da die Parabel in ihrer Scheitelform gegeben ist, lässt sich die y-Koordinate des Scheitels direkt ablesen: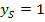

Wegen 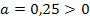ist die Parabel nach oben geöffnet und der Scheitel S ist der Tiefpunkt bzw. das Minimum der Funktion. 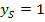ist demnach der kleinstmögliche y-Wert der Funktion 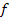. Alle anderen y-Werte sind daher größer als 1. Die Funktion kann somit nur y-Werte annehmen, die größer oder gleich 1 sind.

Die Wertemenge lautet deshalb: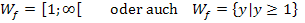

Damit du dir das besser vorstellen kannst, hier der zugehörige Graph:

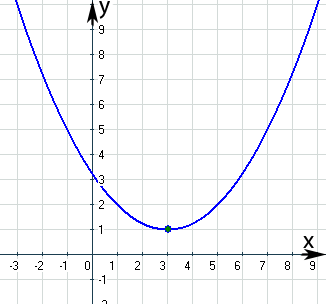
Abb.:Graph der Funktion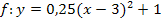

2. Bsp.:

Gib die Wertemenge 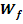der Funktio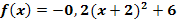n an!

Lösung:

Da die Parabel in ihrer Scheitelform gegeben ist, lässt sich die y-Koordinate des Scheitels direkt ablesen: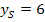

Wegen 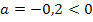ist die Parabel nach unten geöffnet und der Scheitel S ist der Hochpunkt bzw. das Maximum der Funktion. 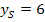ist demnach der größtmögliche y-Wert der Funktion 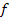. Alle anderen y-Werte sind daher kleiner als 6. Die Funktion kann somit nur y-Werte annehmen, die kleiner oder gleich 6 sind.

Die Wertemenge lautet deshalb: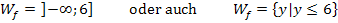

3. Bsp.:

Gib die Wertemenge 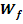der Funktio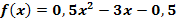n an!

Lösung:

In diesem Beispiel liegt die Parabel noch nicht in Scheitelform vor. Daher kann die y-Koordinate des Scheitels nicht direkt abgelesen werden. Wir müssen die Funktion f zuerst auf Scheitelform bringen. Man kann beispielsweise quadratisch ergänzen. Wie das genau geht, findest du genau erklärt im KapitelQuadratische Ergänzung zur Scheitelberechnung.

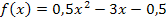
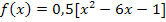
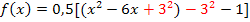
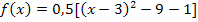
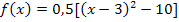
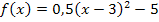
Nun liegt die Funktion f in Scheitelform vor und wir können die y-Koordinate des Scheitels ablesen: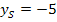

Da a positiv ist, ist die Parabel nach oben geöffnet.

---