Scheitelform einer Parabel

Eine quadratische Funktion kann nicht nur in der Form 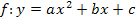, der sogenannten allgemeinen Form, vorliegen, sondern auch in einer als Scheitelform bezeichneten Form. Aus der Scheitelform lässt sich der Scheitel der Parabel sofort ablesen, was in der allgemeinen Form (a,b,c-Form) meist nicht direkt möglich ist.

Scheitelform einer Parabel: 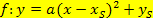mit Scheitel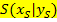

Liegt die Parabel in der Scheitelform vor, ist es ganz leicht, den Scheitel abzulesen:

Wenn man bei der hinteren Zahl in der Klammer das Vorzeichen umdreht, erhält man die x-Koordinate des Scheitels 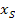. Die Zahl hinter der Klammer entspricht der y-Koordinate des Scheitels 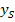. Hier darfst du das Vorzeichen allerdings nicht umdrehen.

Beispiele:

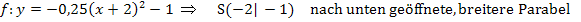
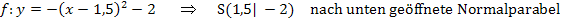
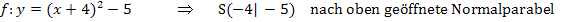
Umwandlung der Scheitelform in die allgemeine Form (a,b,c-Form) der Parabel:

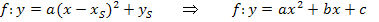
Soll die Scheitelform einer Parabel, also die Form 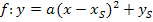, in die allgemeine Form der Parabel, d.h. in die Form 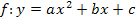, umgewandelt werden, muss zuerst die Klammer mit Hilfe der ersten oder zweiten binomischen Formel quadriert, danach der Faktor a hinein multipliziert und soweit möglich zusammengefasst werden.

Zur Erinnerung:

1. binomische Formel:

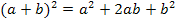
2. binomische Formel:

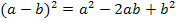
1. Beispiel:

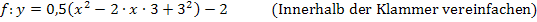
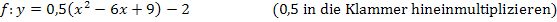
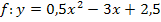
2. Beispiel:

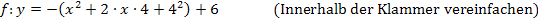
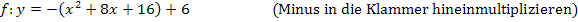
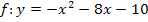
Wie du erkennen kannst, ist es nicht besonders schwer von der Scheitelform zur allgemeinen Form (a,b,c-Form) einer Parabel zu kommen. Eigentlich muss man den Funktionsterm nur ganz normal ausrechnen, dann entsteht automatisch die Form .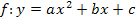

Deutlich schwieriger ist dagegen der umgekehrte Weg, also von der allgemeinen Form 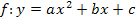zur Scheitelform 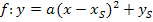. Wie das geht, wird bei der Berechnung des Scheitelpunkts gezeigt.

---