Parabelscharen
Im dritten Fall (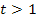 
) gibt es keine Nullstellen. Um die Scharparabel 
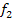zeichnen zu können, muss man entweder den Scheitel berechnen oder eine Wertetabelle erstellen. Die Berechnung des Scheitels geht allerdings schneller. Sie soll hier nicht vorgeführt werden, das kannst du sicher selber. (Falls doch nicht, siehe Berechnung des Scheitelpunktes!) Zur Kontrolle: 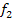hat den Scheitel S(-1|1).
Hier noch einmal die Gleichung der Schar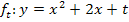 
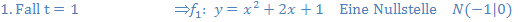
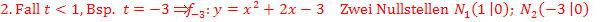
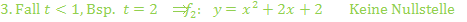
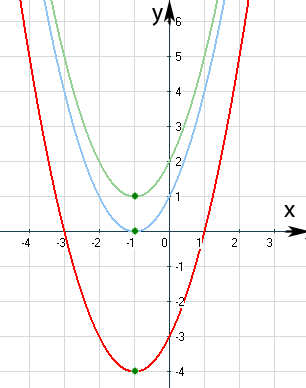
Abb.:Die Graphen der Funktionen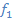 
, 
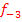und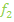 
der Schar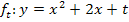
Man erkennt an der Abbildung sofort, dass der Scharparameter t die Parabeln in diesem Beispiel nur nach oben bzw. nach unten verschiebt. Somit ist es auch klar, dass manche Parabeln der Schar die x-Achse zweimal schneiden, andere die x-Achse gar nicht schneiden und eine Scharparabel, nämlich 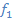, die x-Achse nur berührt. Die Anzahl der Schnittpunkte mit der x-Achse, also die Anzahl der Nullstellen, hängt daher vom Scharparameter t ab. Für welche Werte von t sich nun zwei, eine oder keine Nullstellen ergeben, haben wir in der oben gezeigten Fallunterscheidung ermittelt.
Nun müsste dir eigentlich klar geworden sein, was eine Fallunterscheidung ist. Das Problem mit den Fallunterscheidungen ist meist, dass sie völlig vergessen werden. Vielen Schülern stellt sich jetzt bestimmt die Frage, woran man denn erkennt, dass eine Fallunterscheidung gemacht werden muss. Solange du nur mit Parabelscharen, aber noch nicht mit anderen Scharfunktionen arbeitest, kannst du dir Folgendes merken:Kommt der Scharparameter unter einer Wurzel vor und kann der Ausdruck unter der Wurzel entweder positiv, negativ oder gleich Null sein, dann muss eine Fallunterscheidung gemacht werden! Diese Regel behält auch später, wenn du mit anderen Scharfunktionen arbeiten musst, ihre Gültigkeit. Allerdings wirst du dann auch auf Fallunterscheidungen stoßen, die nichts mit einer Wurzel zu tun haben.
Berechnung der Ortskurve der Scheitelpunkte einer Parabelschar
Ein anderes Problem stellt, neben den Fallunterscheidungen, für viele Schüler die sogenannte Ortskurve der Scheitelpunkte einer Parabelschar dar. Unter der Ortskurve der Scheitelpunkte versteht man die Kurve, auf der alle Scheitelpunkte einer bestimmten Parabelschar liegen. Oder anders gesagt:Würde man nur die Scheitelpunkte der verschiedenen Scharparabeln alle in ein gemeinsames Koordinatensystem einzeichnen, würde man eine bestimmte Kurve, die Ortskurve der Scheitelpunkte, erhalten. Statt der Bezeichnung „Ortskurve“ wird auch der Begriff „Trägergraph“ verwendet. Diese Begriffe sind gleichbedeutend.
