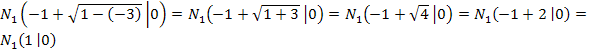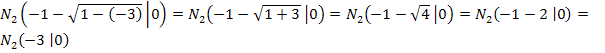Parabelscharen

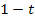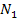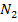Bekanntlich ist die Wurzel aus Null gleich Null, so dass dann beide Nullstellen zusammenfallen, weil es ja egal ist, ob man plus oder minus Null rechnet;man erhält immer das selbe Ergebnis. Nur wenn der Ausdruck positiv ist, ergibt die Wurzel daraus einen positiven Wert. Wegen dem Plus / Minus vor der Wurzel bekommt man dann zwei verschiedene Nullstellen und . Diese Überlegungen führen uns zu der unten gezeigten Fallunterscheidung.

Hier zuerst noch einmal unser letztes Ergebnis: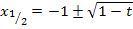

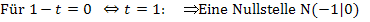
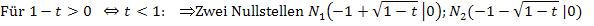
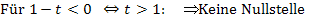
Jetzt ist die Aufgabe wirklich gelöst. Damit du dir allerdings besser vorstellen kannst, was das Ergebnis der Fallunterscheidung eigentlich bedeutet, überlegst du dir am besten zu jedem Fall ein konkretes Beispiel und zeichnest die jeweiligen Scharparabeln. (Das ist natürlich in dieser Aufgabe nicht verlangt, doch solltest du dir die Mühe zumindest dann machen, wenn du noch keine Erfahrung im Umgang mit Funktionenscharen und den dabei vorkommenden Fallunterscheidungen hast.)

Für den ersten Fall (t = 1) berechnest du zuerst die Gleichung der Scharparabel 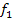. Für den zweiten Fall ( 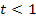) wählst du beispielsweise t = -3, das erfüllt die Bedingung 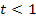und ergibt außerdem schöne Zahlen bei den Nullstellen. Für den dritten Fall ( 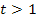) nimmst du zum Beispiel t = 2, weil es die Bedingung 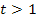offensichtlich erfüllt. Du setzt nun die entsprechenden Werte für t in die Gleichung der Parabelschar 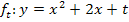ein. Dadurch erhältst du die Gleichungen der Scharparabeln 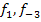und 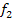. Bei allen Parabeln der Schar 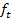handelt es sich um nach oben geöffnete Normalparabeln, da der Öffnungsfaktor a (das ist die Zahl, welche in der Funktionsgleichung vor steht) hier unabhängig von t ist, d.h. a = 1 und das ändert sich auch nicht, egal für welches t. 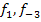Daher sind auch unsere drei Scharparabeln und 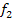nach oben geöffnete Normalparabeln. Man kann sie bequem mit einer Parabelschablone zeichnen. Dazu benötigt man aber entweder die Koordinaten des Scheitels oder die Nullstellen.

Beim ersten Fall (t = 1) kennen wir bereits die Nullstelle N(-1|0). Sie muss zwangsläufig mit dem Scheitel zusammenfallen. Nur wenn der Scheitel von 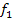genau auf der x-Achse liegt, hat diese Scharparabel genau eine einzige Nullstelle, eben den Scheitel. Somit kann nun der Graph von 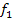leicht gezeichnet werden.

Im zweiten Fall ( 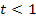) gibt es immer die beiden Nullstellen 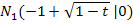und 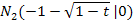. Um unser Beispiel 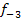zeichnen zu können, setzt man einfach t = -3 in die (in Abhängigkeit von t berechneten) Nullstellen ein.

---