Parabelscharen
Hier noch einmal unsere Gleichung:
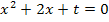
Wir setzen a = 1, b = 2 und c = t in die Mitternachtsformel ein.
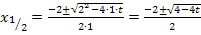
An dieser Stelle werden sich einige Schüler fragen, wie es denn nun weiter geht. Wie soll man denn die Wurzel aus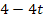 
bloßziehen? Vorsicht:Auf gar keinen Fall darf die Wurzel aus 4 und 
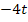einzelnen gezogen werden! Beachte: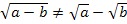 
Ja, aber was nun? Kleiner Tipp:Ausklammern hilft!
Du weißt immer noch nicht, wie es weiter geht. Macht nichts! Also jetzt ganz ausführlich:Wir klammern unter der Wurzel den Faktor 4 aus. Dadurch entsteht nämlich ein Produkt unter der Wurzel und bei Produkten darf die Wurzel einzeln aus den Faktoren gezogen werden.
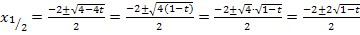
Was hat uns das jetzt gebracht? Wir können nun im Zähler den Faktor 2 ausklammern. Dadurch entsteht ein Produkt, so dass wir kürzen dürfen.
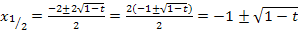
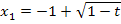
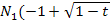|0)
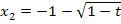
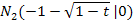
Das sieht doch schon viel besser aus. Der Parameter t kommt, wie erwartet, in der Lösung vor;das stört uns also nicht. Wenn du jetzt aber glauben solltest, dass wir fertig sind, dann liegst du leider falsch. So dürfen wir das nicht stehen lassen. Denn was ist mit der Anzahl der Nullstellen? Du denkst, alle Scharparabeln haben zwei Nullstellen bei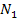 
und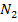 
? Auch das ist leider falsch! Die Anzahl der Nullstellen unserer Scharparabeln hängt nämlich noch von t ab. Wir müssen eine Fallunterscheidung machen. In diesem Beispiel wurde schon in der Aufgabenstellung auf die nötige Fallunterscheidung hingewiesen;das ist jedoch in Prüfungen bei den meisten Aufgaben nicht der Fall, was oft dazu führt, dass die notwendige Fallunterscheidung vom Schüler komplett vergessen wird.
Merke:Immer wenn der Scharparameter unter einer Wurzel auftaucht, ist Vorsicht geboten! Oft muss dann eine Fallunterscheidung gemacht werden.
Wie du sicher weißt, kann aus einer negativen Zahl keine Wurzel gezogen werden. Wir müssen uns daher überlegen, für welche Werte von t die Wurzel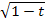 
überhaupt definiert ist. Dein Lehrer in der Schule würde vermutlich sagen:„Der Radikand darf nicht negativ sein!“ Mit dem Radikand ist der Ausdruck unter der Wurzel, hier 
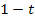, gemeint und das darf eben nicht negativ sein. Wird der Ausdruck 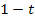negativ, ist die Wurzel gar nicht definiert und es existieren somit keine Nullstellen. Ergibt sich für 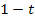genau der Wert Null, kann die Wurzel zwar gezogen werden, doch existiert dann nur eine Nullstelle.
