Parabelscharen

Nun schauen wir uns ein relativ einfaches, rein mathematisches Beispiel einer Parabelschar genauer an. Hieran soll auch ein erstes Mal gezeigt werden, wie man denn nun „in Abhängigkeit von k“ rechnet.

1. Bsp.:

Ermittle die Nullstellen der Parabelschar 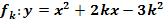in Abhängigkeit von k!

Lösung:

Wie du weißt, handelt es sich bei den Nullstellen einer Funktion um die Schnittpunkte ihres Graphen mit der x-Achse. Alle Punkte, welche auf der x-Achse liegen, haben die y-Koordinate y = 0. Daher berechnet man die Nullstellen, indem man für y die Zahl 0 einsetzt, was dem Nullsetzen der Funktionsgleichung entspricht. Wir setzen deshalb die gegebene Funktionsgleichung der Parabelschar gleich Null. Den Scharparameter k stellen wir uns dabei einfach als irgendeine feste Zahl vor. Da in der Aufgabenstellung nichts bezüglich k angegeben ist, gilt:k ℝ

y = 0

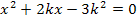
Nun liegt eine gemischtquadratische Gleichung mit der Variablen x vor. Die Gleichung ist gemischtquadratisch, weil die Variable x sowohl zum Quadrat als auch ohne Potenz vorkommt. Dass die Gleichung gemischtquadratisch ist, hat aber nichts damit zu tun, dass auch der Scharparameter k mit und ohne Quadrat enthalten ist. Das ist in dieser Aufgabe zwar zufälligerweise auch der Fall, aber entscheidend ist die Variable x! Wir müssen schließlich nach x auflösen, wenn wir die Nullstellen ermitteln wollen. Wenn dir das nicht wirklich klar ist, denke dir doch einmal für k den Wert 2 oder 3. Wie würdest du denn dann weiter rechnen? Du würdest natürlich die Mitternachtsformel anwenden, um nach x aufzulösen, weil es sich eben um eine gemischtquadratische Gleichung (= Gleichung mit und x) handelt. Wir dürfen natürlich nicht wirklich für k eine konkrete Zahl einsetzen;wir sollen ja in Abhängigkeit von k rechnen! Doch denken müssen wir uns trotzdem:k ist bloßeine Zahl. Wir rechnen nun also entsprechend weiter und setzen in die Mitternachtsformel ein. Den Scharparameter k nehmen wir einfach in unserer Rechnung mit, so als wenn k eben eine Zahl wäre.

Zur Erinnerung:

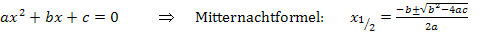
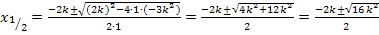
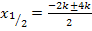
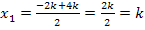
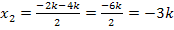
Die Nullstellen der Parabelschar lauten und 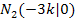. Im Endergebnis kommt noch der Scharparameter k vor. Das war aber zu erwarten, da wir schließlich in Abhängigkeit von k rechnen sollten. Es soll allerdings noch darauf hingewiesen werden, dass bei dieser Aufgabe im Fall k = 0 nicht zwei verschiedene Nullstellen vorliegen, sondern nur eine einzige (doppelte) Nullstelle, da sich für k = 0 bei beiden Nullstellen 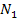und 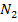jeweils (0|0) ergibt.

---