Parabelscharen
– Allerdings erhält man je nach Wahl des Scharparameters a breitere bzw. schmälere Parabeln. Sie können nach oben geöffnet sein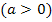 
oder nach unten 
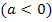. Das kannst du leicht nachvollziehen, indem du für a eine bestimmte Zahl einsetzt, dann eine Wertetabelle erstellst und die jeweilige Scharparabel zeichnest. Danach wählst du einen anderen Wert für a, machst wieder eine Wertetabelle und zeichnest die nächste Scharparabel in das Koordinatensystem, worin du schon die erste Parabel gezeichnet hast. So verfährst du nun mit weiteren Werten von a. Also immer für a einen konkreten Zahlenwert einsetzen, dann Wertetabelle machen und zeichnen. Schneller und einfacher geht es natürlich mit einem Graphiktaschenrechner oder einem Computer, doch ist es gar keine schlechte Übung, zumindest mit zwei oder drei verschiedenen Werten von a das Ganze einmal selber durchzurechnen und selber die verschiedenen Parabeln der Schar zu zeichnen. Wenn du noch nie mit Funktionenscharen, z.B. mit Geradenscharen, zu tun hattest, solltest du dir die Mühe einmal machen. Dadurch erhältst du eine Zeichnung, ähnlich der folgenden Abbildung. Es hängt natürlich davon ab, welche Werte du für a gewählt hast. So können deine Scharparabeln natürlich eine andere „Breite“ haben als die hier abgebildeten.
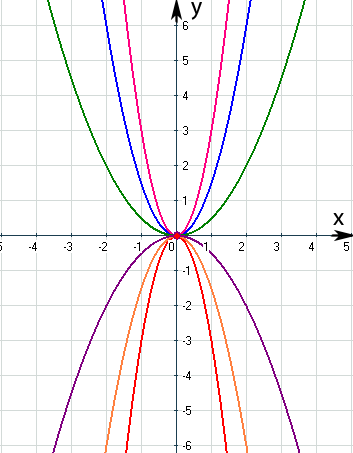
Abb.:Einige Graphen der Schar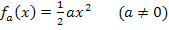 
Hoffentlich ist dir nun der Unterschied zwischen Variablen wie x, y bzw. t, v und dem Scharparameter a klar geworden. An der Funktionsgleichung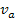 
(t) = … oder 
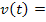… erkennt man die Variablen v und t übrigens schon daran, dass sie normalgroßgeschrieben sind, während der Scharparameter a entweder kleiner und tiefergestellt (als Index) geschrieben ist oder sogar auf der linken Seite der Funktionsgleichung gar nicht auftaucht.
Wie du an dem Beispiel mit der beschleunigten Bewegung sehen konntest, ist gerade bei dem Buchstaben t besondere Vorsicht geboten. In physikalischen Aufgaben steht t für die Variable „Zeit“, wogegen in rein mathematischen Aufgaben t als Scharparameter, also als Konstante verwendet wird.
TIPP:Beim Rechnen mit Scharen stellst du dir den Scharparameter, nennen wir ihn nun wie schon in unserem ersten Beispiel wieder k, am besten als konkrete Zahl vor. Solltest du ´mal gar nicht mehr weiter wissen, wenn du eigentlich in Abhängigkeit von k rechnen sollst, hilft es oft, sich zu fragen, wie man die selbe Rechnung durchführen würde, wenn der Scharparameter k zum Beispiel den Wert 2 oder 3 hätte. An Stelle der Zahlen 2 oder 3 kannst du dir natürlich jede beliebige Zahl denken. Die Zahlen 2 und 3 wurden nur vorgeschlagen, weil sie zwar relativ einfach, aber auch nicht zu einfach sind. Die Zahlen 1 und 0 eignen sich dagegen nicht, weil sie meist zu unzulässigen Vereinfachungen führen.
