Parabelscharen
h. sie soll sich während dieses Versuches nicht ändern, weil es sich um eine Bewegung mit konstanter Beschleunigung handelt. Die Geschwindigkeit v ändert sich natürlich mit der Zeit t, aber diese Änderung soll immer gleich sein. Der Körper wird also immer gleich stark beschleunigt (oder abgebremst).
Nehmen wir beispielsweise den Fall eines mit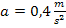 
konstant beschleunigten Körpers an. Dann berechnet sich seine Geschwindigkeit 
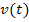zum Zeitpunkt t (also nach t Sekunden seit Beginn der Bewegung) mit der Formel:
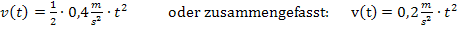
Setzt man nun für t verschiedene Werte (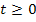 
, denn die Zeit t kann nicht negativ sein, der Versuch startet ja erst bei t = 0) in die Funktion 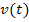ein, erhält man die jeweiligen Geschwindigkeiten des Körpers zu dem entsprechenden Zeitpunkt. Du siehst daran, t und v sind hier variabel, sie ändern sich während dieses konkreten Versuchs. Je nach dem, was man für t in 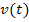einsetzt, erhält man ein anderes v. Die Beschleunigung a war aber bei diesem konkreten Versuch immer konstant, hat sich also nicht verändert. Wir wollten schließlich eine Bewegung mit konstanter Beschleunigung a untersuchen. Für ein neues Experiment kann a natürlich einen anderen Wert annehmen. Aber auch für dieses neue Experiment bleibt die Beschleunigung a dann während des ganzen Versuchs unverändert, also a = konstant. Die Geschwindigkeit v ändert sich dagegen natürlich wieder mit der Zeit t;der Körper wird ja konstant beschleunigt. Das mit der wirklich konstanten Beschleunigung a ist natürlich in der Praxis nicht machbar, aber was soll´s, hier sollen schließlich nur Parabelscharen einführend erklärt werden.
Die Gleichung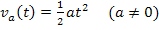 
stellt nämlich eine Schar von Parabeln dar. (Genau genommen nur den rechten Ast der Parabeln, da die Zeit t nicht negativ sein kann.) Dass es sich um eine Parabelschar handelt, erkennt man leichter, wenn man sich überlegt, dass dem t eigentlich x entspricht und in der Mathematik statt 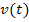meist 
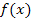geschrieben wird. Dann sähe das Ganze folgendermaßen aus:
Nun kannst du am Vorkommen von 
in der Funktionsgleichung als höchste Potenz von x leicht erkennen, dass es sich um Parabeln handelt. Damit wir jeweils nicht nur den rechten Ast der Parabeln erhalten, sehen wir das Ganze ´mal als rein mathematisches Beispiel und erweitern die Definitionsmenge auf alle reellen Zahlen. Dann können wir auch negative Werte für x einsetzen und wir erhalten komplette Parabeln. Alle Parabeln der Schar haben (unabhängig von a) ihren Scheitel im Ursprung. – Unabhängig von a bedeutet dabei, dass es immer so ist, egal was man für a einsetzt.
