Parabelscharen

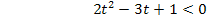
Die Lösung dieser quadratischen Ungleichung kann ebenfalls aus der obigen Skizze abgelesen werden. Wir lesen einfach die Bereiche auf der t-Achse ab, wo die Hilfsparabel 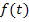unterhalb der t-Achse liegt. So erhält man:

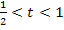
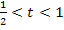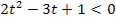Für gilt , also 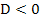und somit existieren dann keine gemeinsamen Punkte der Scharparabel 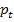mit der Geraden .

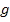Damit ist die Aufgabe gelöst. Wir fassen unsere Ergebnisse nur noch einmal übersichtlich zusammen.

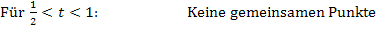
Falls du an Stelle der Ungleichungsdarstellung für t lieber die Intervallschreibweise verwendest, hier noch die andere Schreibweise:

Für t 1 gemeinsamer Punkt

Für t ℝ 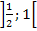2 gemeinsame Punkte

Für t 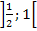Keine gemeinsamen Punkte

Zwei weitere Beispielaufgaben mit Parabelscharen findest du im Kapitel Lagebeziehungen zwischen zwei Parabeln (Bsp. 4 und 5). Dies waren hoffentlich genügend Beispiele zu diesem Thema.

---