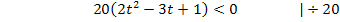Parabelscharen
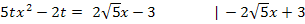
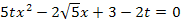
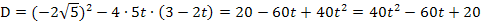
Man kann jetzt noch den Faktor 20 ausklammern. Dadurch werden die Zahlen etwas handlicher. (Das muss aber nicht gemacht werden.)
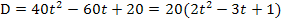
In dieser Form erkennt man ganz leicht, dass keine binomische Formel vorliegt.
Die Diskriminante lässt sich also nicht mehr weiter vereinfachen. Wir müssen nun untersuchen, für welche Werte von t die Diskriminante gleich Null, positiv oder negativ wird, um herauszufinden, für welche Werte von t sich genau ein, zwei bzw. kein gemeinsamer Punkt der Parabelschar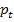 
mit der Geraden 
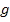ergibt.
Wir beginnen mit dem einfachsten Fall, nämlich D = 0.
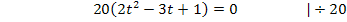
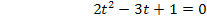
Es ist nun wieder eine gemischtquadratische Gleichung zu lösen. Wir müssen jetzt aber natürlich nach t auflösen;eine andere Unbekannte kommt ja gar nicht mehr vor. Wir benützen die Mitternachtsformel, wobei t hier dem x aus der allgemeinen Form der gemischtquadratischen Gleichung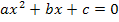 
entspricht.
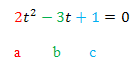
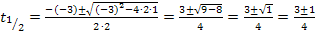
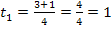
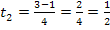
Für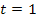 
oder 
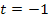ergibt sich genau ein gemeinsamer Punkt.
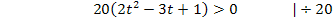
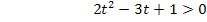
Nun stehen wir vor dem Problem, dass wir eine gemischtquadratische Ungleichung lösen müssen. Wir wählen dafür die graphische Methode, da sie wesentlich einfacher ist als die rechnerische. (Ausführlich erklärt werden diese Lösungsmethoden im Bereich Algebra im Kapitel Quadratische Ungleichungen.) Wir stellen uns die linke Seite der Ungleichung als Parabel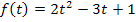 
vor. Es handelt sich um eine nach oben geöffnete Parabel mit den Nullstellen 
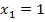und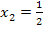 
. Die Nullstellen kennen wir, da wir im 1. Fall bereits die Gleichung 
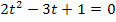gelöst haben und das entspricht ja der Berechnung der Nullstellen der Parabel 
.
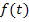Es ist wichtig zu unterscheiden zwischen der angegebenen Parabelschar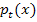 
und der Parabel 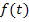. Die neue Parabel 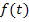ist nur eine Hilfsfunktion, die uns dazu dient die quadratische Ungleichung zu lösen. Sie hat nicht direkt mit der gegebenen Schar von Parabeln zu tun.
Wir skizzieren nun die Hilfsfunktion 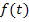mit Hilfe ihrer Nullstellen 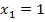und .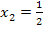
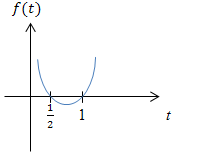
Um die quadratische Ungleichung zu lösen, braucht man nun nur noch aus der Skizze ablesen, für welche Werte von t die Parabel 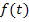oberhalb der t-Achse liegt, da 
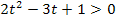nichts anderes bedeutet als 
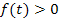, und das bedeutet wiederum nichts anderes als, dass die y-Werte von 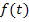positiv sein sollen, also dass die Hilfsparabel 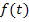oberhalb der t-Achse liegen soll. Wir lesen nun einfach aus der Skizze die entsprechenden Werte von t ab:
Für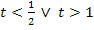 
gilt 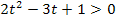, also 
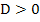und somit liegen dann zwei gemeinsame Punkte der Scharparabel 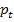mit der Geraden 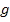vor.
