Parabelscharen
Damit du leichter erkennen kannst, was in unserer Gleichung den Koeffizienten a, b und c entspricht, hier das Ganze noch einmal mit Farben dargestellt:
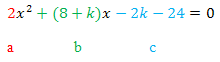
Um die Anzahl der Lösungen zu ermitteln, benötigen wir die Diskriminante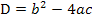 
.
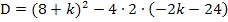
Wir vereinfachen, indem wir die vordere Klammer mit der ersten binomischen Formel auflösen,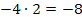 
in die hintere Klammer hineinmultiplizieren und soweit möglich zusammenfassen.
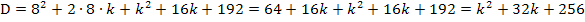
In der Diskriminante kommt der Parameter zum Quadrat vor. Daher überlegen wir uns, ob nicht zufälligerweise, wie schon im vorherigen Beispiel, eine binomische Formel vorliegt.
Zur Erinnerung:
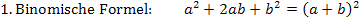
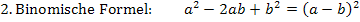
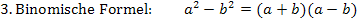
Es liegt die Vermutung nahe, dass es sich bei dem Ausdruck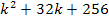 
um die erste binomische Formel handelt, denn erstens passen die Vorzeichen zur ersten binomischen Formel und vor allem ist 256 eine Quadratzahl, es ist nämlich 
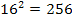. Auch das gemischte Glied passt, denn 
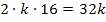. Es liegt also wirklich die erste binomische Formel vor.
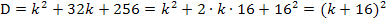
So, das sieht doch schon ´mal ganz gut aus. Wegen des Quadrats um die Klammer kann D niemals negativ werden. Es gilt daher:
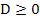für k 
ℝ
Deshalb existiert immer mindestens eine Lösung, also mindestens ein gemeinsamer Punkt der Scharparabel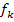 
und der Parabel h. Genau das war zu beweisen.
Leider funktioniert der Trick mit der binomischen Formel nicht immer. Wenn in der Diskriminante der Scharparameter zum Quadrat, aber trotzdem keine binomische Formel vorliegt, ergibt sich das Problem, dass eine quadratische Ungleichung zu lösen ist. Wie das gemacht wird, kannst du im nächsten Beispiel sehen. Habt ihr im Unterricht noch keine quadratischen Ungleichungen behandelt, musst du das folgende Beispiel allerdings noch nicht lösen können.
5. Bsp.:
Für welche Werte von t hat die Parabelschar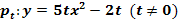 
mit der Geraden 
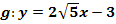genau einen, genau zwei bzw. gar keinen Punkt gemeinsam?
Lösung:
Diese Aufgabe hat es in sich! Du denkst vielleicht, dass es wegen der Wurzel zu Schwierigkeiten kommen kann. Doch das ist gar nicht das Problem. Wie gerade erwähnt, stellen vielmehr quadratische Ungleichungen die Schwierigkeit dar. Noch kann man das nicht erkennen. Zuerst müssen wir die Parabelschar mit der Geraden wieder gleichsetzen. Es ergibt sich dabei, wie schon bei den vorherigen Beispielen, eine gemischtquadratische Gleichung, die wir natürlich erst auf die Form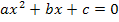 
bringen müssen. Weil nach der Anzahl der gemeinsamen Punkte gefragt ist, muss die Diskriminante D gebildet werden. Soweit noch kein Problem;das kannst du auch gleich ´mal selbst versuchen, ohne dir vorher die folgende Lösung anzuschauen.
