Parabelscharen
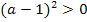
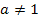
Jetzt sind wir eigentlich fertig. Das Ergebnis der Fallunterscheidung wird nur noch einmal zusammengefasst.
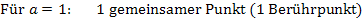
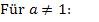2 gemeinsame Punkte (2 Schnittpunkte)
Es müsste dir jetzt klar geworden sein, wie entscheidend es war, dass sich die Diskriminante hier mit Hilfe der binomischen Formel zum Schluss noch einmal umformen ließ. Ohne diese Umformung hätte man nicht sofort erkennen können, dass D gar nicht negativ sein kann. Jetzt denkst du dir vielleicht:„Dass man da eine binomische Formel anwenden kann, das hätte ich alleine nie erkannt!“ Deshalb gleich noch einmal ein Beispiel, bei dem dieser Trick funktioniert. Klar, das geht nicht immer. Aber oftmals machen die Lehrer gerade in der 9.Klasse die Aufgaben so, dass es funktioniert.
Merke:Falls in der Diskriminante der Parameter zum Quadrat auftaucht, immer überprüfen, ob nicht etwa eine binomische Formel vorliegt!
Wenn du Probleme hast, zu erkennen, ob eine binomische Formel vorliegt, wiederhole zuerst unbedingt das Kapitel Binomische Formeln.
4. Bsp.:
Zeige, dass die Parabelschar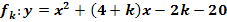 
für alle k 
ℝ mit der Parabel 
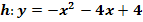mindestens einen Punkt gemeinsam hat!
Lösung:
Im Prinzip wird diese Aufgabe nach dem gleichen Weg gelöst wie schon die Aufgabe im 3. Bsp. Dass nun eine Parabelschar und eine weitere Parabel an Stelle der Geraden vorliegen, ändert am Rechenweg nichts. Auf jeden Fall muss in Abhängigkeit von k gerechnet werden. Wir dürfen also keinesfalls irgendeine konkrete Zahl für k einsetzen, sondern müssen einfach mit k rechnen, als wäre es eine Zahl. Wir setzen die Parabelschar zuerst mit der anderen Parabel gleich. Es ergibt sich eine gemischtquadratische Gleichung. Daher bringen wir, wie schon in den vorherigen Beispielen, alles auf eine Seite der Gleichung. Dann fassen wir durch geschicktes Ausklammern alle Faktoren zusammen, die 
enthalten, und alle die nur x enthalten. Es wird natürlich nach absteigender Potenz von x geordnet, damit man besser erkennen kann, was den Koeffizienten a, b und c aus der Mitternachtsformel bzw. Diskriminantenformel entspricht. Dann muss nur gezeigt werden, dass die Diskriminante nicht negativ werden kann, egal, was für k eingesetzt wird, da es mindestens eine Lösung geben soll. Versuche es doch gleich ´mal alleine! Zu deiner Kontrolle oder, falls du nicht weiter weißt, folgt hier natürlich der ausführliche Rechenweg.
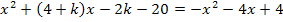
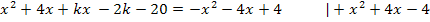
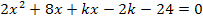
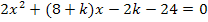
Es liegt nun eine gemischtquadratische Gleichung in der Form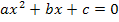 
vor.
