Parabelscharen
Da es uns um die Anzahl der Lösungen dieser Gleichung geht, berechnen wir die Diskriminante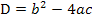 
.
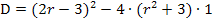
Um die Diskriminante zu vereinfachen, müssen die Klammern aufgelöst werden. Die hintere Klammer kann ganz normal ausmultipliziert werden. (Achtung:Vorzeichen beachten!) Um die erste Klammer zu quadrieren, verwendet man am besten die zweite binomische Formel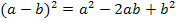 
.
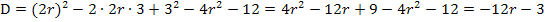
In unserer Diskriminante kommt der Scharparameter r vor. Je nach dem, was für r eingesetzt wird, erhält man verschiedene Ergebnisse für D. Die Diskriminante D kann positiv, gleich Null oder negativ werden. Es hängt deshalb vom Scharparameter r ab, wie viele Lösungen / gemeinsame Punkte sich ergeben.
Nun muss eine Fallunterscheidung gemacht werden, weil es eben von r abhängt, ob die Diskriminante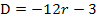 
positiv, gleich Null oder negativ ist.
Zur Erinnerung:
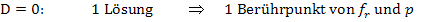
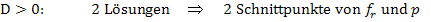
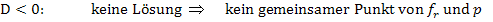
Je nach dem, was man für r einsetzt, kann sich für D schließlich ein positiver oder negativer Wert oder auch genau Null ergeben. Unsere Aufgabe ist es jetzt herauszufinden, für welche Werte von r die Diskriminante 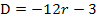positiv, gleich Null bzw. negativ wird.
Im Allgemeinen ist es am einfachsten, mit D = 0 zu beginnen, da sich hierbei eine Gleichung und keine Ungleichung ergibt, und eine Gleichung ist für die meisten Schüler einfacher zu lösen als eine Ungleichung. In diesem Fall sind zwar auch die Ungleichungen leicht zu lösen, da hier kein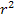 
in der Diskriminante vorkommt. (In anderen Aufgaben, siehe 3. bis 5. Bsp., ist das allerdings anders, was uns zum Problem der quadratischen Ungleichungen führt.) Wir beginnen unsere Fallunterscheidung mit dem Fall D = 0.
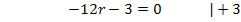
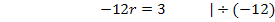
Für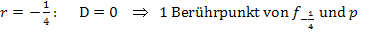 
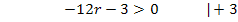
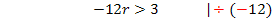
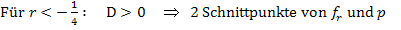
Beachte, dass sich bei der Division durch -12 (negative Zahl!) das Ungleichheitszeichen umdreht! Bei Ungleichungen gilt immer die Regel, dass sich das Ungleichheitszeichen umdreht, wenn mit einer negativen Zahl multipliziert oder durch eine negative Zahl dividiert wird. (Diese Regel wird als Inversionsgesetz bezeichnet.)
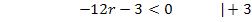
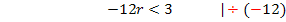
Für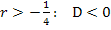 
Keine gemeinsamen Punkte von 
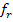und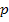 
Jetzt sind wir eigentlich fertig. Wir fassen, der Übersicht wegen, nur noch unsere Ergebnisse zusammen:
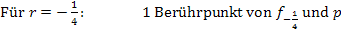
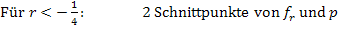
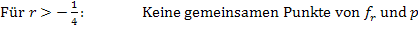
Die soeben vorgeführte Fallunterscheidung gehört zu den einfacheren, da keine quadratische Ungleichung zu lösen war. Im gerade gezeigten Beispiel enthielt die Diskriminante D den Parameter nicht zum Quadrat. Daher ließen sich die Ungleichungen, die in den Fällen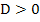 
bzw.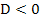 
entstanden, noch recht leicht nur durch Äquivalenzumformungen (d.h. Umstellen der Gleichung) lösen. Wie du allerdings bei Fallunterscheidungen vorgehst, wenn der Parameter auch zum Quadrat in der Diskriminante vorkommt, wird in den folgenden Beispielen gezeigt.
