Parabelscharen
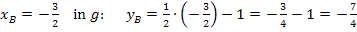
So, nun sind wir (endlich) fertig! Die Koordinaten des gesuchten Berührpunktes der Scharparabel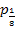 
mit der Geraden 
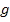lauten 
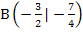bzw. B(-1,5|-1,75).
Diese Aufgabe war sicherlich nicht ganz einfach für dich. Leider wird es nicht leichter, wenn wir uns nun mit Aufgaben beschäftigen, bei denen eine Fallunterscheidung gemacht werden muss. Doch auch Fallunterscheidungen können unterschiedlich schwer sein. Die folgenden Aufgabenbeispiele sollen dich Schritt für Schritt auch an schwierigere Fallunterscheidungen heranführen. Wir beginnen aber mit einem relativ einfachen Beispiel. Versuche es doch gleich ´mal alleine die folgende Aufgabe zu lösen, also ohne vorher die Lösung anzuschauen! (Die Aufgabe ist auch wirklich nicht so schwer. Die Fallunterscheidung funktioniert im Prinzip genauso wie schon vorher bei der Berechnung der Nullstellen einer Parabelschar. Vergleiche oben!)
2. Bsp.:
Überprüfe die Lage der Parabelschar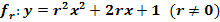 
bezüglich der Parabel 
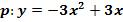in Abhängigkeit von r! (Fallunterscheidung!)
Lösung:
Die Aufgabe hätte auch anders formuliert werden können:Für welche Werte von r existieren zwei, genau ein oder gar kein gemeinsamer Punkt der beiden Funktionen? Um diese Frage beantworten zu können, müssen wir die Parabelschar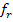 
zuerst mit der Parabel 
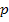gleichsetzen. Dadurch erhalten wir die folgende Gleichung:
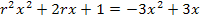
Die Gleichung ist gemischtquadratisch, weil sie neben 
auch x ohne Potenz enthält. Wir müssen sie auf die Form 
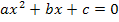bringen, d.h. wir müssen alles auf eine Seite der Gleichung bringen. Wir stellen also entsprechend um und ordnen dabei, wie gewöhnlich, nach absteigender Potenz von x.
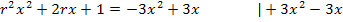
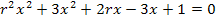
Nun stehst du vermutlich vor dem Problem, dass du nicht weißt, wie du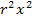 
mit 3 und 
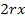mit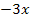 
zusammenfassen kannst. An dieser Stelle wissen die meisten Schüler nicht weiter. Denk´dir also nichts dabei, wenn du an dieser Stelle nicht weiter gewusst hast. Der Trick dabei ist eigentlich ganz einfach, nur wissen muss man ihn! Man muss nur geschickt ausklammern, dann ist das Problem gelöst. Genauer gesagt, wird aus 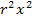und 3 jeweils ausgeklammert und entsprechend aus 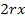und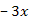 
das x.
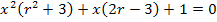
Nun drehen wir noch jeweils die Reihenfolge der einzelnen Faktoren um, d.h. wir schreiben jeweils bzw. x hinter die entsprechende Klammer, und schon haben wir die Gleichung in der gewünschten Form vorliegen.
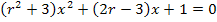
Damit du leichter erkennen kannst, was in der vorliegenden Gleichung dem a, b und c entspricht, das Ganze noch einmal farbig dargestellt.
