Parabelscharen
Merke:Immer wenn es um die Anzahl der Lösungen einer gemischtquadratischen Gleichung geht, nicht die ganze Mitternachtsformel anwenden, sondern nur die Diskriminante D berechnen!
Zur Erinnerung:
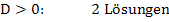
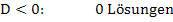
Hier noch einmal die Gleichung, welche wir erhalten haben durch das Gleichsetzen der beiden Funktionen:
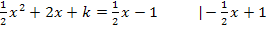
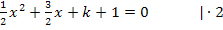
Wir multiplizieren mit dem Faktor 2, damit die Brüche wegfallen. Das muss man nicht unbedingt machen, es erleichtert jedoch die weitere Rechnung. Wer rechnet denn schon gerne mit Brüchen, wenn es auch ohne geht? Also besser mit dem Hauptnenner, also in diesem Fall mit dem Faktor 2, multiplizieren! Die rechte Seite der Gleichung bleibt Null, da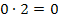 
ist.
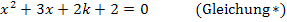
Nun kann die Diskriminante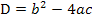 
berechnet werden. Damit es dir leichter fällt, zu erkennen, was hier a, b bzw. c entspricht, noch einmal unsere Gleichung, aber mit farbig dargestellten Koeffizienten a, b und c.
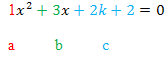
D =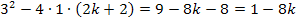 
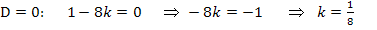
Für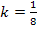 
ergibt sich also eine Parabel, die mit der Geraden 
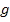genau einen gemeinsamen Punkt besitzt. Die Gerade ist also Tangente an die Parabel 
.
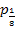Nun soll noch der Berührpunkt für diesen Fall ermittelt werden. Dazu muss nicht erst für k der Wert 
in die Parabelschar 
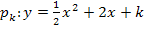eingesetzt und wieder mit der Geraden 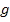gleichgesetzt werden. Wir können nämlich einfach die Rechnung von oben verwenden. Da haben wir ja schon einmal gleichgesetzt, zwar in Abhängigkeit von k, aber das macht nichts. Wir können schließlich jetzt den Wert für k in die Gleichung* einsetzen. Dadurch sparen wir uns viel unnötige Arbeit.
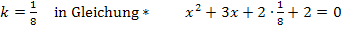
Jetzt wenden wir die (ganze) Mitternachtsformel an. Wir wollen ja nach x auflösen und nicht etwa die Anzahl der Lösungen berechnen. Deshalb verwenden wir jetzt nicht nur die Diskriminante, sondern die komplette Mitternachtsformel.
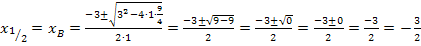
Die Diskriminante ergibt den Wert Null. Daher erhalten wir genau eine Lösung, was natürlich zu erwarten war, da wir k schließlich so bestimmt haben, dass sich genau ein gemeinsamer Punkt ergibt. (Indem wir die Diskriminante gleich Null gesetzt haben, haben wir ja berechnet, dass 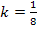sein muss, damit sich die beiden Funktionen berühren. Daher muss jetzt auch wieder Null für die Diskriminante herauskommen.)
Nun muss nur noch die y-Koordinate des Berührpunktes B berechnet werden. Dazu kann man entweder in die Gleichung der Parabelschar für k den Wert und für x die x-Koordinate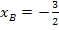 
einsetzen oder einfach 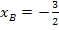für x in die Geradengleichung 
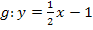einsetzen. Wir entscheiden uns für den bequemeren, also den zuletzt genannten Weg und setzen in die Geradengleichung ein.
