Parabelscharen
Egal, was man für k einsetzt, die y-Koordinate von S bleibt immer gleich, nämlich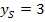 
. (Nur die x-Koordinaten von S ändern sich, je nach dem, was für k eingesetzt wird.) Weil 
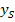unabhängig ist von k, kann die Gleichung der Ortskurve der Scheitelpunkte sofort, also ohne weitere Rechnung, angegeben werden. Wir lassen einfach den Index S bei der y-Koordinate des Scheitels 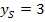weg und erhalten so die gesuchte Ortskurve. Die Ortskurve der Scheitel hat also die Gleichung y = 3. Es handelt sich dabei um eine waagrechte Gerade, genauer gesagt, um eine im Abstand 3 zur x-Achse parallel verlaufende Gerade.
Rechnerische Überprüfung der Lagebeziehung eine Parabelschar und einer Gerade oder einer anderen Parabel
Ein weiterer häufig verlangter Aufgabentyp ist die rechnerische Überprüfung der Lagebeziehung eine Parabelschar und einer Gerade oder einer anderen Parabel. Wie schon bei der Berechnung der Nullstellen einer Parabelschar, ist hierbei wieder häufig eine Fallunterscheidung nötig.
Etwas einfacher sind Aufgaben, in denen verlangt ist, dass der Scharparameter so bestimmt werden soll, dass die Parabelschar beispielsweise nur einen gemeinsamen Punkt mit einer angegebenen Gerade oder einer anderen Parabel hat. Schauen wir uns doch gleich einmal so eine Aufgabe an.
1. Bsp.:
Gegeben sind die Parabelschar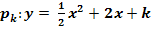 
und die Gerade 
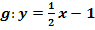. Für welchen Wert von k ist die Gerade 
Tangente an 
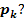Gib für diesen Fall auch die Koordinaten des Berührpunktes B an!
Lösung:
Wie bereits im Kapitel Lagebeziehungen zwischen Parabel und Gerade ausführlich besprochen, ist eine Gerade nur dann Tangente an eine Parabel, wenn sie genau einen gemeinsamen Punkt mit der Parabel hat. Gemeinsame Punkte zweier Funktionen berechnet man immer, indem man die beiden Funktionen gleichsetzt. Daher setzen auch wir als erstes einmal die Parabelschar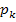 
mit der Geraden 
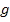gleich. So erhalten wir die folgende Gleichung:
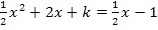
Es handelt sich um eine gemischtquadratische Gleichung, also um eine Gleichung mit 
und x (ohne Potenz). Bekanntlich lassen sich solche Gleichungen mit der Mitternachtsformel lösen. Diese kann jedoch erst angewendet werden, wenn die Gleichung in der Form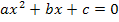 
vorliegt. Wir müssen unsere Gleichung daher entsprechend umstellen, d.h. alles auf eine Seite der Gleichung bringen, damit … = 0 da steht, bevor wir die Diskriminante D bilden können. Wir verwenden nicht sofort die ganze Mitternachtsformel, sondern berechnen zuerst nur die Diskriminante 
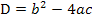, da wir schließlich daran interessiert sind, für welche Werte von k sich genau eine Lösung ergibt. (Die Gerade soll ja Tangente an die Parabel sein.) Die Diskriminante muss den Wert Null besitzen, damit die Mitternachtsformel genau eine Lösung ergibt.
