Parabelscharen
3. Bsp.:Gegeben ist die Parabelschar 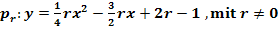 . Gib die Gleichung der Ortskurve der Scheitelpunkte an!
. Gib die Gleichung der Ortskurve der Scheitelpunkte an!
Lösung:
Wie im vorherigen Beispiel müssen wir zuerst den Scheitel in Abhängigkeit vom Scharparameter, hier r genannt, ermitteln. Da die Parabelschar noch nicht in ihrer Scheitelform angegeben ist, können wir den Scheitel leider nicht direkt ablesen.
Versuche doch gleich ´mal selbst den Scheitel in Abhängigkeit von r zu berechnen! (Genaueres unter:Berechnung des Scheitelpunkts) Gymnasiasten der Mittelstufe müssen die Quadratische Ergänzung (zur Scheitelberechnung) verwenden. Gymnasiasten ab der 11. Klasse berechnen den Scheitel, das Extremum der Parabel, indem sie die erste Ableitung gleich Null setzen. Realschüler können stattdessen auch die Formel zur Scheitelberechnung benützen;das ist wesentlich einfacher und geht viel schneller. Im Folgenden wird, wie schon im Beispiel vorher, die kompliziertere quadratische Ergänzung vorgeführt.
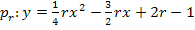
![]()
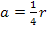 ausklammern
ausklammern  Durch
Durch 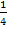 und durch r teilen, d.h. mit dem Kehrwert von
und durch r teilen, d.h. mit dem Kehrwert von 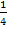 , also
, also 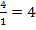 multiplizieren und durch r teilen
multiplizieren und durch r teilen
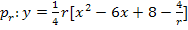
![]() Quadratische Ergänzung:Ausdruck vor dem x halbieren und quadrieren, zuerst + dann gleich wieder – rechnen
Quadratische Ergänzung:Ausdruck vor dem x halbieren und quadrieren, zuerst + dann gleich wieder – rechnen
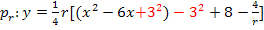
![]()
2. Binomische Formel anwenden und beginnen den hinteren Teil auszurechnen. Vorsicht:Das Quadrat bei 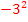 bezieht sich nur auf die 3, nicht aber auf das Minus-Zeichen. So erhält man:
bezieht sich nur auf die 3, nicht aber auf das Minus-Zeichen. So erhält man:
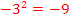
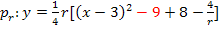
![]() Zusammenfassen
Zusammenfassen
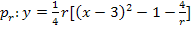
![]() Eckige Klammer auflösen
Eckige Klammer auflösen
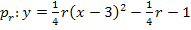
![]() Scheitelkoordinaten ablesen
Scheitelkoordinaten ablesen
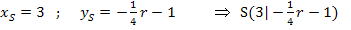
Hier liegt nun der Sonderfall vor, dass die x-Koordinate des Scheitels den Scharparameter r nicht enthält. Daher kann die Gleichung der Ortskurve ohne weitere Rechnung direkt abgelesen werden. Sie hat einfach die Gleichung x = 3, da schließlich alle Scheitelpunkte der Schar  die gleiche x-Koordinate, nämlich
die gleiche x-Koordinate, nämlich  = 3, haben. (Die y-Koordinate der Scheitel enthält dagegen den Parameter r;sie ändern sich also, je nach dem was für r eingesetzt wird.) Die Scheitelpunkte liegen deshalb alle auf der senkrechten Gerade x = 3.
= 3, haben. (Die y-Koordinate der Scheitel enthält dagegen den Parameter r;sie ändern sich also, je nach dem was für r eingesetzt wird.) Die Scheitelpunkte liegen deshalb alle auf der senkrechten Gerade x = 3.
Nun noch ein letztes Beispiel, bei dem die y-Koordinate des Scheitels unabhängig ist vom Scharparameter.
4. Bsp.:Gib die Gleichung der Ortskurve der Scheitelpunkte der Parabelschar 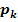 an!
an!
Lösung:
Die Parabelschar liegt bereits in Scheitelform vor. Die Koordinaten des Scheitelpunktes können (in Abhängigkeit von k) direkt abgelesen werden.
Scheitel 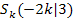
Die y-Koordinate des Scheitels ist unabhängig vom Scharparameter k, d.h. bei der y-Koordinate des Scheitels kommt kein k vor.

