Parabelscharen

Ab der 11. Klasse bietet es sich an, den Scheitel wie ein Extremum zu berechnen, d.h. die Ableitung 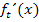zu bilden und gleich Null zu setzen. (Vergleiche:Scheitelberechnung mit Hilfe der Differenzialrechnung)

Da vielen Schülern die quadratische Ergänzung, die leider von vielen Lehrern in der Mittelstufe gefordert wird, erfahrungsgemäßanfangs Probleme bereitet, soll dieser Lösungsweg im Folgenden vorgeführt werden. Gehst du in die 9. Klasse eines Gymnasiums, musst du sowieso zwangsläufig auf diesen Lösungsweg zurückgreifen. (Ab der 11. Klasse kann der Scheitel dann, wie gesagt, wesentlich bequemer mit Hilfe der Differenzialrechnung ermittelt werden.)

Du solltest die Quadratische Ergänzung (zur Scheitelberechnung), zumindest ohne Parameter, einigermaßen beherrschen, bevor du dich mit der Lösung dieser Aufgabe beschäftigst.

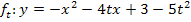
a = -1 (d.h. das Minus-Zeichnen) ausklammern Vorzeichen umdrehen

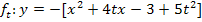
Quadratische Ergänzung:Ausdruck vor dem x halbieren und quadrieren, zuerst + dann gleich wieder – rechnen

=

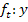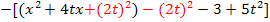
1. Binomische Formel anwenden und beginnen den hinteren Teil auszurechnen. Vorsicht:Das Quadrat bei 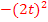bezieht sich nur auf 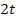, nicht aber auf das Minus-Zeichen. So erhält man:

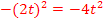
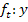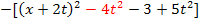= Zusammenfassen

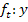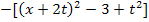
= Eckige Klammer auflösen

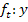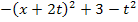
= Scheitelkoordinaten ablesen

)

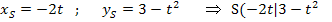Nun kann die Ortskurve der Scheitelpunkte ermittelt werden.

I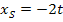

II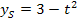

Wir lösen Gleichung I nach t auf und setzen das Ergebnis für t in Gleichung II ein.

I

I´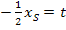

I´in II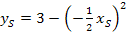

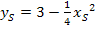
Jetzt muss nur noch der Index, also der tiefergestellte, kleiner geschriebene Buchstabe S, weggelassen werden und die Ortskurve der Scheitelpunkte ist ermittelt.

Ortskurve der Scheitelpunkte: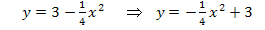

Es handelt sich bei dieser Ortskurve der Scheitelpunkte um eine nach unten geöffnete, breitere (mathematisch gesagt:in y-Richtung gestauchte) Parabel. Damit man das besser erkennt, ordnen wir die Gleichung der Ortskurve nach fallenden Potenzen von x. (Wir ordnen schließlich bei allen Parabeln immer nach absteigender Potenz von x: als erstes, dann x – das fehlt hier – dann als letztes die Zahl ohne x.) Aber Vorsicht beim Umtauschen der Reihenfolge:Die Vorzeichen der jeweiligen Faktoren musst du natürlich „mitnehmen“. Damit ist gemeint, dass das Minus vor 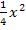stehen bleiben muss und das Plus vor der 3.

Die Ortskurve 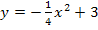gehört selbst nicht zur Parabelschar 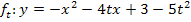, da es sich bei allen Scharparabeln um nach unten geöffnete Normalparabeln handelt. Eine breitere Parabel, wie die Ortskurve kann daher nicht zur Schar gehören.

---