Parabelscharen

Sollte dir die Vorgehensweise zur Ermittlung der Ortskurve der Scheitelpunkte noch nicht wirklich klar sein, ist das nicht weiter schlimm. An Hand der folgenden Beispiele wird sich hoffentlich gleich alles klären. Schauen wir uns zu jedem Fall ein konkretes Beispiel an.

1. Bsp.:

Gegeben ist die Parabelschar 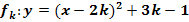. Ermittle die Gleichung der Ortskurve der Scheitel der Schar !

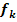Lösung:

Zuerst müssen wir den Scheitel in Abhängigkeit vom Scharparameter k ermitteln. Da die Parabelschar schon in ihrer Scheitelform angegeben ist, können wir – ohne weitere Rechnung – den Scheitel ablesen.

Zur Erinnerung:

Scheitelform einer Parabel:

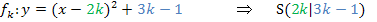
Wir kennen nun die Koordinaten des Scheitels in Abhängigkeit von k:

x-Koordinate des Scheitels: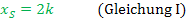

y-Koordinate des Scheitels: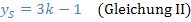

Beide Koordinaten des Scheitels enthalten den Scharparameter k. Daher müssen wir den Parameter k eliminieren. Wir lösen dazu Gleichung I nach k auf und setzen dann das Ergebnis für k in Gleichung II ein.

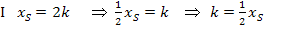
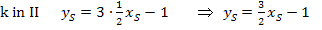
Jetzt muss nur noch der Index (= der tiefergestellte, kleiner geschriebene Buchstabe) S weggelassen werden und wir haben die Gleichung der Ortskurve berechnet.

Ortskurve der Scheitel: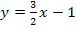

Man erkennt, dass eine Funktion der Form vorliegt. Wie du weißt, handelt es sich dabei immer um lineare Funktionen, also Geraden, mit der Steigung m und dem y-Achsenabschnitt t. Die Ortskurve der Scheitelpunkte ist in diesem Beispiel also eine Gerade mit der Steigung m = 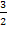und dem y-Achsenabschnitt t = -1. Auf dieser Geraden liegen daher alle Scheitelpunkte der Schar 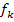. (Wenn du das Thema „Geraden“ wiederholen möchtest, gehe zu Lineare Funktionen/Geraden!) In der folgenden Abbildung sind einige Parabeln der Schar 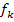und die Ortskurve 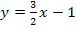dargestellt. Du siehst:Alle Scheitelpunkte der abgebildeten Scharparabeln liegen auf dieser Gerade.

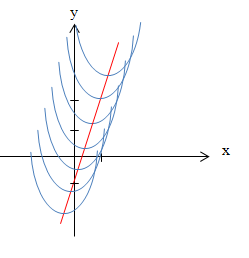
Abb.:Einige Parabeln der Schar 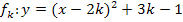mit der Ortskurve der Scheitel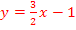

2. Bsp.:

Gegeben ist die Parabelschar 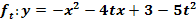. Ermittle die Gleichung der Ortskurve der Scheitel der Schar !

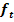Lösung:

Zuerst müssen wir den Scheitel in Abhängigkeit vom Scharparameter t ermitteln. Da die Parabelschar noch nicht in ihrer Scheitelform angegeben ist, können wir den Scheitel nicht direkt ablesen.

Wie du den Scheitel berechnest, bleibt dir selbst überlassen, wenn du versuchen möchtest diese Aufgabe alleine zu lösen. Du kannst, wie im Kapitel Berechnung des Scheitelpunkts bereits ausführlich beschrieben, beispielsweise die Quadratische Ergänzung (zur Scheitelberechnung) verwenden, oder, wenn du auf eine Realschule gehst, die Formel zur Scheitelberechnung.

---