Parabelscharen
Betrachte noch einmal die oben gezeigte Abbildung der Graphen von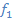 
, 
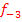und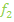 
der Schar 
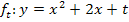. Es wird dir sicher auffallen, dass alle Scheitelpunkte in diesem Beispiel auf einer senkrechten Gerade, also auf einer Parallelen zu y-Achse im Abstand 2 (nach links) liegen. Genau diese Gerade ist die Ortskurve der Scheitelpunkte der Schar 
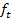. Sie hat die Gleichung 
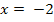. Das ist aus der Zeichnung leicht ersichtlich.
Da stellen sich nun allerdings einige Fragen:Sind alle Ortskurven senkrechte Geraden oder zumindest irgendwelche Geraden? Und vor allem:Wie findet man die Gleichung einer Ortskurve rechnerisch?
Ortskurven sind natürlich nicht immer Geraden, sonst würden sie ja „Ortsgeraden“ heißen! Eine Ortskurve kann zwar, wie im oben gezeigten Beispiel, eine Gerade sein, kann aber auch, wie der Name schon sagt, eine richtige Kurve, also eine gebogene Linie, sein. So können die Scheitelpunkte einer Parabelschar beispielsweise auf einer Parabel liegen. Ob diese Parabel dann ebenfalls zur Schar gehört, kann nicht allgemeint beantwortet werden. Das kann im Einzelfall so sein;in der Regel handelt es sich aber um eine ganz andere Funktion. Um diese Frage beantworten zu können, muss zuerst die Gleichung der Ortskurve ermittelt werden. An der Gleichung der Ortskurve erkennt man dann auch, ob eine Gerade, eine Parabel oder eine andere Art von Kurve vorliegt.
Anleitung zur Berechnung der Ortskurve der Scheitelpunkte (= Trägergraph der Scheitelpunkte):
· Scheitelkoordinaten in Abhängigkeit vom Scharparameter berechnen
· Falls sowohl bei der x- als auch bei y-Koordinate des Scheitels der Scharparameter vorkommt, gehst du folgendermaßen vor:
Die Gleichung, welche die x-Koordinate des Scheitelpunkts angibt, nach dem Scharparameter auflösen und in die andere Gleichung, welche die y-Koordinate des Scheitels angibt, für den Scharparameter einsetzen (Das nennt man mathematisch gesprochen „den Scharparameter eliminieren“.)
· Falls entweder die x-Koordinate oder y-Koordinate des Scheitels unabhängig ist vom Scharparameter, d.h. eine der beiden Scheitelkoordinaten ist eine richtige Zahl und enthält den Scharparameter gar nicht:
1. Möglichkeit:
Die x-Koordinate des Scheitels enthält keinen Scharparameter (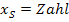 
)
Die Ortskurve der Scheitel ist eine senkrechte Gerade mit der Gleichung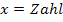 
2. Möglichkeit:
Die y-Koordinate des Scheitels enthält keinen Scharparameter (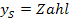 
)
Die Ortskurve der Scheitel ist eine waagrechte Gerade mit der Gleichung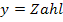 
· Wenn der Scharparameter weder in der x-Koordinate noch in der y-Koordinate des Scheitels vorkommt, d.h. der Scheitel ist unabhängig vom Scharparameter, haben alle Parabeln der Schar den selben Scheitelpunkt und es gibt gar keine Ortskurve.
