Parabeln zeichnen

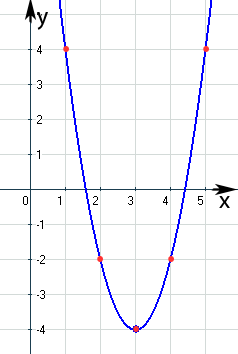
Abb.:Graph der Funktion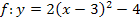

2. Bsp.:

Zeichne den Graph der Funktion 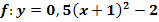in ein Koordinatensystem!

Lösung:

Die Parabel ist wieder in ihrer Scheitelform gegeben, daher kann der Scheitel sofort abgelesen werden.

Scheitel S(-1|-2)

Als erstes zeichnet man den Scheitelpunkt in das Koordinatensystem ein. Der Öffnungsfaktor a der Parabel ist in diesem Beispiel a = 0,5. Da a positiv ist, liegt wieder eine nach oben geöffnete Parabel vor, welche wegen 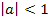breiter als die Normalparabel ist. Man geht nun vom Scheitelpunkt aus 1 nach rechts (und auch nach links) und jeweils um 1 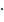0,5 = 0,5 nach oben, dann wieder vom Scheitel aus 2 nach rechts (und auch nach links) und jeweils um 4 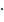0,5 = 2 nach oben, danach 3 nach rechts (und auch nach links) und jeweils um 9 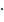0,5 = 4,5 nach oben. Zum Schluss werden wieder alle Punkte weich miteinander verbunden. Fertig ist die Parabel!

Abb.:Graph der Funktion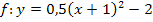

3. Bsp.:

Zeichne den Graph der Funktion 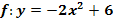in ein Koordinatensystem!

Lösung:

Die Parabel liegt in diesem Beispiel zwar nicht in ihrer Scheitelform vor, sondern in der allgemeinen Form 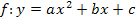, da aber der Koeffizient b = 0 ist (d.h. x ohne Quadrat fehlt) kann der Scheitel trotzdem direkt abgelesen werden.

Zur Erinnerung:

Eine Parabel der Form 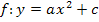ist um c nach oben 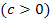bzw. um c nach unten 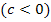verschoben. Zur Seite ist sie nicht verschoben. Der Scheitelpunkt ist bei S(0|c).

Die Parabel 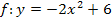ist um 6 nach oben verschoben. Zur Seite verschoben ist sie wegen b = 0 nicht. Daher liegt der Scheitel bei S(0|6).

Wir zeichnen wieder zuerst den Scheitelpunkt in das Koordinatensystem ein. Der Öffnungsfaktor a der Parabel ist in diesem Beispiel a = -2. Da a negativ ist, liegt eine nach unten geöffnete Parabel vor, die wegen 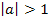schmäler als die Normalparabel ist. Man geht nun vom Scheitelpunkt aus 1 nach rechts (und auch nach links) und jeweils um 1 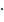2 = 2 nach unten, dann wieder vom Scheitel aus 2 nach rechts (und auch nach links) und jeweils um 4 2 = 8 nach unten, danach 3 nach rechts (und auch nach links) und jeweils um 9 2 = 18 nach unten (wenn das Koordinatensystem überhaupt großgenug ist.) Nun verbindet man alle Punkte weich miteinander und fertig ist die Parabel.

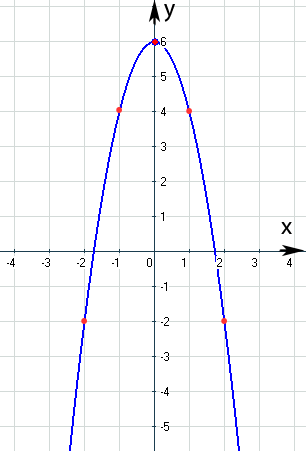Abb.:Graph der Funktion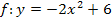

Wenn dir dieses Verfahren zu kompliziert erscheint, erstellst du besser immer eine Wertetabelle und zeichnest die Parabel auf diese Art und Weise;das ist sicherer.

Verwende das gerade erläuterte Verfahren ohne Wertetabelle nur dann, wenn du es wirklich gut beherrschst!

---