Parabeln zeichnen
2. Methode:Ohne Wertetabelle
Vielleicht hast du bereits im Unterricht gesehen, dass dein Lehrer breitere oder schmälere Parabeln auch ohne Wertetabelle ganz schnell zeichnen kann. Wie das funktioniert, wird im Folgenden erklärt.
Als erstes muss der Scheitel der Parabel ermittelt werden, denn von diesem Punkt gehen wir aus, um die Parabel zu zeichnen. Wie der Scheitel gefunden werden kann, wird im Kapitel Berechnung des Scheitelpunkts ausführlich erläutert. Als erstes zeichnen wir also den Scheitel S(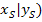 
der Parabel 
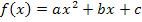bzw.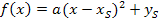 
in ein Koordinatensystem ein. Nun gehen wir ähnlich vor, als wollten wir eine Normalparabel ohne Schablone zeichnen. Siehe oben! Bei einer nach oben geöffneten Normalparabel würde man vom Scheitel 1 nach rechts (bzw. nach links) und 1 nach oben gehen, dann 2 nach rechts (bzw. nach links) und 4 nach oben, danach 3 nach rechts (bzw. nach links) und 9 nach oben gehen usw. Ist die Parabel nach unten geöffnet, geht man entsprechend nicht nach oben sondern nach unten. Bei breiteren bzw. schmäleren Parabeln müssen wir zusätzlich den Öffnungsfaktor a miteinbeziehen. Ist a positiv, ist die Parabel nach oben geöffnet und wir gehen vom Scheitel 1 nach rechts (bzw. nach links) und 1 
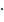a nach oben, dann 2 nach rechts (bzw. nach links) und 4 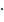a nach oben, danach 3 nach rechts (bzw. nach links) und 9 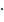a nach oben usw. Ist die Parabel nach unten geöffnet, geht man entsprechend nicht nach oben sondern nach unten. Um das Vorgehen zu verdeutlichen, folgen mehrere konkrete Beispiele
.
1. Bsp.:
Zeichne den Graph der Funktion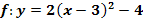 
in ein Koordinatensystem!
Lösung:
Da die Parabel in ihrer Scheitelform vorliegt kann der Scheitel sofort abgelesen werden.
Scheitel S(3|-4)
Man zeichnet als erstes den Scheitelpunkt in ein Koordinatensystem ein. Der Öffnungsfaktor a der Parabel ist in diesem Beispiel a = 2. Da a positiv ist, liegt eine nach oben geöffnete Parabel vor, die wegen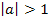 
schmäler als die Normalparabel ist. Wir brauchen also auf der y-Achse mindestens 5 cm nach unten, weil die y-Koordinate des Scheitels bei -4 liegt. Nach oben braucht man auf der y-Achse mindestens 7 cm. (Du kannst natürlich auch noch mehr Platz nach oben einplanen.) Die x-Koordinate des Scheitels liegt bei 
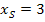. Daher brauchen wir auf der x-Achse vom Scheitel ausgehend mindestens 2 cm, besser 3cm nach links und rechts. Man geht nun vom Scheitelpunkt aus 1 nach rechts (und auch nach links) und jeweils um 1 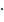2 = 2 nach oben, dann wieder vom Scheitel aus 2 nach rechts (und auch nach links) und jeweils um 4 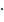2 = 8 nach oben, danach 3 nach rechts (und auch nach links) und jeweils um 9 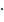2 = 18 nach oben (wenn überhaupt so viel Platz im Koordinatensystem ist.) Nun können alle Punkte weich miteinander verbunden werden und die Parabel ist fertig eingezeichnet.
