Parabeln zeichnen
unten, je nachdem ob die Parabel nach oben bzw. nach unten geöffnet ist, und markierst diesen Punkt. Dann gehst du wieder vom Scheitel aus 2 nach rechts und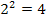 
nach oben bzw. unten. Entsprechend geht es weiter:Wieder vom Scheitel aus 3 nach rechts und 
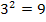nach oben bzw. nach unten;dann würde es mit 4 nach rechts und 
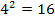nach oben bzw. unten weitergehen, doch dann wird wohl der Platz im Koordinatensystem knapp. Nun könntest du bereits den einen Ast der Parabel zeichnen;den anderen Ast erhältst du entweder durch Spiegelung der markierten Punkte an der Symmetrieachse der Parabel, die schließlich senkrecht durch den Scheitel verläuft, oder du trägst die Punkte die du vorher nach rechts gegangen bist, noch einmal nach links ein. Also vom Scheitel ausgehend 1 nach links und 1 nach oben/unten, dann 2 nach links und 4 nach oben/unten, danach 3 nach links und 9 nach oben/unten usw.
Nun können alle Punkte weich miteinander verbunden werden. Keinesfalls dürfen die einzelnen Punkte mit dem Geodreieck oder Lineal durch gerade Linien verbunden werden. Eine Parabel hat keine „Ecken“ oder „Knicke“! Also immer frei Hand zeichnen, wenn keine entsprechende Schablone vorhanden ist! Lieber wackelig, aber frei mit der Hand gezeichnet, als mit dem Lineal zwar „schön“, aber falsch gezeichnet. Es gilt wirklich als Fehler, die Parabel mit einem Lineal zu zeichnen!
Breitere oder schmälere Parabeln (gestauchte oder gestreckte Parabeln) zeichnen:
1. Methode:Wertetabelle erstellen
Am einfachsten ist es zu Beginn für dich wahrscheinlich eine Wertetabelle anzulegen und mit Hilfe der berechneten Kurvenpunkte die Parabel zu zeichnen. Dazu ist es aber wichtig, einen geeigneten Bereich auszuwählen. Es stellt also die Frage, wie man so einen Bereich findet. Sinnvoll erscheinen Bereiche, die symmetrisch zur x-Koordinate des Scheitels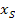 
liegen. Als Faustregel gilt: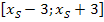 
Ist die Parabel jedoch wesentlich breiter als die Normalparabel empfiehlt sich jedoch ein etwas größerer Bereich, beispielsweise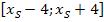 
oder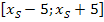 
.
Ist die Parabel umgekehrt wesentlich schmäler als die Normalparabel, wählt man besser ein kleineres Intervall, zum Beispiel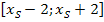 
, da sonst die y-Werte der berechneten Kurvenpunkte schnell zu hoch zum Einzeichnen in ein Koordinatensystem mit dem Maßstab 1LE =1 cm werden. Natürlich können auch abweichende Maßstäbe verwendet werden, z. B. auf der x-Achse 1 LE = 1 cm und auf der y-Achse 1LE = 0,5 cm.
