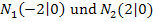Nullstellen einer quadratischen Funktion
h. eine Gleichung der Form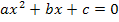 
( 
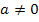). Wie man quadratische Gleichungen rechnerisch lösen kann, wird ausführlich im Kapitel Rechnerische Verfahren zur Lösung quadratischer Gleichungen im Bereich Algebra behandelt.
1. Bsp.:Berechne die Nullstellen der Funktion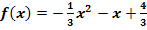 
Lösung:
Nst.: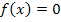 
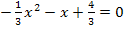
Um diese gemischtquadratische Gleichung (Gleichung mit 
und x) zu lösen, kann entweder sofort die Mitternachtsformel angewendet werden oder vorher noch mit dem Hauptnenner, in diesem Fall mit der Zahl 3, multipliziert werden. Durch das Multiplizieren mit dem Faktor 3 vereinfachen sich die Zahlen erheblich;man hat dann keine Brüche mehr.
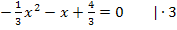
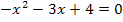
Achtung:Die rechte Seite der Gleichung bleibt 0, weil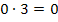 
Mitternachtsformel anwenden:
 |
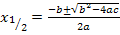
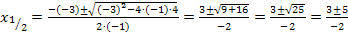
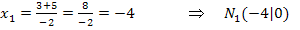
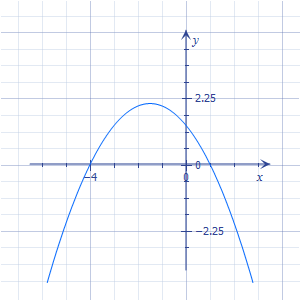Abb.:Graph der Funktion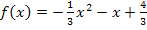 
mit den Nullstellen 
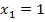und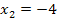 
2. Bsp.: Berechne die Nullstellen der Funktion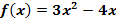 
Lösung:
Nst.: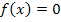
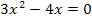
Diese Gleichung ist zwar wie im ersten Beispiel gemischtquadratisch, weil sie sowohl als auch x (ohne Potenz) enthält, sie kann aber, anstatt mit der Mitternachtsformel, auch einfach durch Ausklammern von x gelöst werden, da keine Konstante (Zahl ohne x) vorkommt. Wir können deshalb x ausklammern und bekommen so auf der linken Seite der Gleichung ein Produkt. Da ein Produkt gleich Null ist, wenn einer der Faktoren gleich Null ist, dürfen dann die beiden Faktoren des Produkts, also x und die Klammer, einzeln gleich Null gesetzt werden.
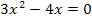
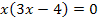
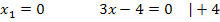
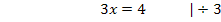
Die Nullstellen liegen also bei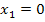 
und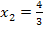 
. Die Schnittpunkte mit der x-Achse lauten 
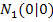und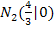 
.
Anmerkung:Dasselbe Ergebnis hätte man erhalten, wenn man die Mitternachtsformel verwendet hätte. Dabei gilt zu beachten, dass mit c = 0 gerechnet werden muss, da die Konstante c in der Gleichung 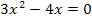fehlt. Die Verwendung der Mitternachtsformel ist jedoch wesentlich zeitaufwendiger und daher nicht zu empfehlen!
3. Bsp.: Berechne die Nullstellen der Funktion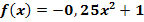 
!
Lösung:
Nst.: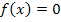
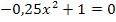
Diese Gleichung ist reinquadratisch, d.h. sie enthält neben kein weiteres x. Solche Gleichungen werden gelöst, indem man isoliert, also auf eine Seite und die Zahl auf die andere Seite der Gleichung bringt, und danach falls möglich die Wurzel zieht. (Achtung:Aus negativen Zahlen kann man die Wurzel nicht ziehen. In so einem Fall gäbe es keine Nullstellen.) Vergiss außerdem nicht das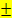 
vor der Wurzel!
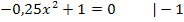
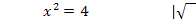
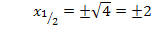
Die Nullstellen lauten: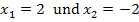 
.
Schnittpunkte der Parabel mit der x-Achse: 
