Nullstellen einer quadratischen Funktion
Unter den Nullstellen einer Funktion (abgekürzt Nst.) versteht man, wie du weißt, die x-Koordinaten der Schnittpunkte mit der x-Achse. Man kann die Nullstellen einer quadratischen Funktion, also einer Parabel, graphisch ermitteln, indem man die Parabel beispielsweise mit Hilfe einer Wertetabelle zeichnet und aus der Zeichnung die x-Koordinaten der Schnittpunkte des Graphen mit der x-Achse abliest. Allerdings führt die graphische Methode nicht zu wirklich exakten Werten für die Nullstellen.
Genaue Lösungen erhält man nur auf rechnerischem Weg. Doch wie berechnet man nun die Nullstellen einer Funktion? Du hast das wahrscheinlich schon einmal gelernt, doch wiederholen wir besser kurz die Grundlagen:Jeder Punkt, der auf der x-Achse liegt, hat die y-Koordinate y = 0, da man ja nicht in y-Richtung nach oben oder unten geht. (Wenn dir das nicht ganz klar ist, stelle dir einfach einige Punkte auf der x-Achse vor und überlege dir ihre Koordinaten. Dabei wirst du feststellen, dass alle Punkte die y-Koordinate y = 0 haben. Die Gleichung der x-Achse lautet deshalb y = 0.) Um die Nullstellen einer Funktion zu berechnen, setzt man daher für y die Zahl Null in die Funktionsgleichung ein. Das entspricht dem Gleich-Null-Setzen des Funktionsterms.
Merke:Die Nullstellen einer Funktion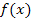 
werden berechnet, indem man y bzw. 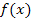gleich Null setzt.
Nullstellen: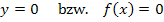 
Dadurch dass man die quadratische Funktion gleich Null gesetzt hat, erhält man eine quadratische Gleichung, d.
