Lagebeziehungen zwischen zwei Parabeln

Hinweis:

In diesem Kapitel wird vorausgesetzt, dass du gemischtquadratische Gleichungen rechnerisch lösen kannst. (Das sind Gleichungen, die sowohl als auch x ohne Exponent enthalten.) Du solltest mit der „Mitternachtsformel“ bzw. mathematisch korrekt „Lösungsformel für gemischtquadratische Gleichungen“ umgehen können. Kannst du dich nicht mehr wirklich daran erinnern, wiederhole besser erst das Kapitel Gemischtquadratische Gleichungen!

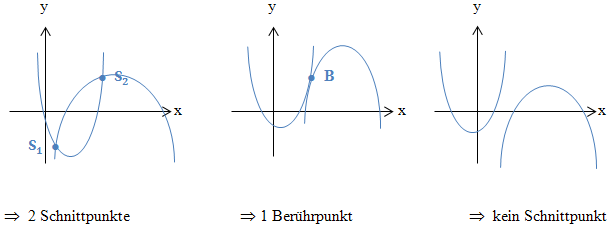
Mögliche Lagebeziehungen zwischen zwei Parabeln:

Zwei Parabeln können sich in zwei verschiedenen Punkten schneiden.

Eine Parabel kann eine andere Parabel in genau einem Punkt berührt.

Zwei Parabeln können auch gar keinen gemeinsamen Punkt haben.

Rechnerische Überprüfung der Lagebeziehungen zwischen zwei Parabeln:

Wie gerade besprochen, unterscheidet man je nach Anzahl der gemeinsamen Punkte der beiden Parabeln die folgenden drei Fälle:

· Die Parabeln schneiden sich in zwei verschiedenen Schnittpunkten 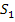und .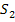

· Die Parabeln haben nur einen Punkt gemeinsamen, den Berührpunkt B. Achtung:So ein Punkt wird nicht als Schnittpunkt, sondern immer als Berührpunkt bezeichnet. Die Parabeln schneiden sich nicht, sondern berühren sich nur.

· Die Parabeln haben keinen gemeinsamen Punkt.

Im Prinzip rechnen wir wie bei der Überprüfung der Lagebeziehungen zwischen Parabel und Gerade. Wir versuchen wieder eventuell vorhandene gemeinsame Punkte der beiden Funktionen zu finden. Um die gemeinsamen Punkte zweier Parabeln 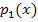und 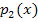zu berechnen, setzt man die beiden Parabeln gleich und löst – falls möglich – nach x auf. In der Regel entsteht durch das Gleichsetzen der beiden Funktionen 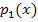und 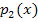eine gemischtquadratische Gleichung, d.h. eine Gleichung, die und x ohne Exponent enthält. Solche Gleichungen werden am besten mit der sogenannten „Mitternachtsformel“ gelöst. Damit die „Mitternachtsformel“ angewendet werden kann, muss die Gleichung aber zuerst auf die Form 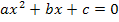gebracht werden.

---