Lagebeziehungen zwischen Parabel und Gerade
Zuerst setzen wir die Gleichung der Parabel mit der Gleichung der Geradenschar gleich, so wie wir es bereits bei den vorherigen Beispielen gemacht haben. Lass dich nicht dadurch stören, dass hier eine Geradenschar und nicht eine konkrete Gerade vorliegt. Wir tun einfach so als wäre m eine konkrete Zahl.
Hier noch einmal die Angaben: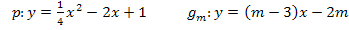 
Parabel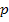 
und Geradenschar 
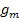gleichsetzen und nach Null auflösen, damit die Mitternachtsformel zur Lösung der gemischtquadratischen Gleichung (Gleichung mit 
und x) verwendet werden kann:
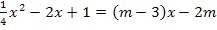
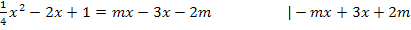
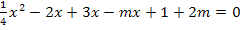
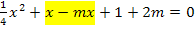(Linke Seite nach absteigenden Potenzen von x geordnet!)
Damit die Mitternachtsformel angewendet bzw. die Diskriminante später berechnet werden kann, muss die Gleichung aber in der Form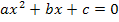 
vorliegen. Nach Null haben wir bereits aufgelöst;die linke Seite der Gleichung passt aber noch nicht ganz. Es ist zwar bereits nach absteigenden Potenzen von x geordnet, also zuerst der Ausdruck mit , dann die Ausdrücke mit x und zuletzt alles ohne x, aber was entspricht in dieser Gleichung dem a, b und c aus der Mitternachtsformel? So wie die Gleichung im Moment geschrieben ist, erkennt man das sehr schlecht. Daher wenden wir einen kleinen Trick an:Wir klammern aus den Ausdrücken, die nur x aber kein enthalten, das x aus. Das machen wir, weil wir x und –mx nicht anders zusammenfassen können! Merke dir dieses Vorgehen, denn du wirst es in anderen Aufgaben mit Scharen noch öfter brauchen!
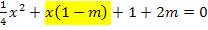
Den Ausdruck in der Klammer stellst du dir einfach als konkrete Zahl vor, da m eine konkrete Zahl darstellt, steht auch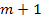 
für eine bestimmte Zahl. Weil wir es gewohnt sind Zahl 
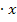(z.B.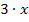 
) und nicht 
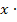Zahl (z.B. 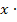3) zu schreiben, drehen wir die Reihenfolge des gelb unterlegten Ausdrucks um. Außerdem setzen wir der Übersichtlichkeit wegen eine Klammer um alles, was kein x enthält. Nun kann man besser erkennen, was in dieser Gleichung dem a, b und c aus der Mitternachtsformel entspricht.
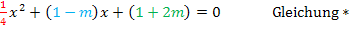
a
b c
In Teilaufgabe a.) ist danach gefragt, für welchen Wert von m sich eine Tangente an die Parabel ergibt. Eine Tangente hat bekanntlich mit der Parabel genau einen gemeinsamen Punkt, also einen Berührpunkt. Unsere Gleichung darf daher nur eine Lösung besitzen. Das ist dann der Fall, wenn die Diskriminante D den Wert Null annimmt.
Tangente ⇔ D = 0
Wir berechnen deshalb die Diskriminante D in Abhängigkeit von m. Das bedeutet, man rechnet einfach mit m, als wäre m eine Zahl, ohne aber für m etwas einzusetzen. m soll also im Ergebnis der Diskriminante noch vorkommen!
