Lagebeziehungen zwischen Parabel und Gerade
Danach lösen wir nach Null auf, d.h. wir bringen alles auf eine Seite, damit wir die Mitternachtsformel zur Lösung der Gleichung verwenden können. Genauer gesagt, muss eigentlich nur die Diskriminante D berechnet werden. Wir wollen schließlich zeigen, dass es keine gemeinsamen Punkte von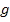 
und 
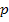gibt. Daher kann die durch das Gleichsetzen entstehende Gleichung gar keine Lösung besitzen. Wir müssen also zeigen, dass die Diskriminante D negativ ist.
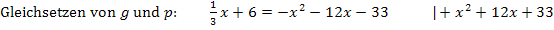
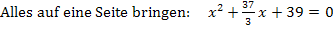
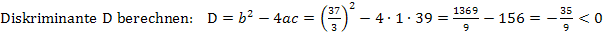
Die Diskriminante ist negativ. Daher gibt es keine gemeinsamen Punkte, was zu zeigen war.
Das folgende Beispiel ist nur für Schüler eines Gymnasiums, der FOS / BOS oder einer Realschule (mathematischer Zweig) ab der 9. Klasse geeignet, da es eine Geradenschar beinhaltet. Für Realschüler anderer Zweige in Bayern nicht Schulstoff!
4. Bsp.:
Gegeben sind die Parabel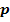 
und die Geradenschar 
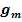. Für welche Werte von m ist die Gerade 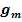Tangente an die Parabel 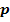? Gib auch die Gleichung dieser Tangenten und die Koordinaten der jeweiligen Berührpunkte B an!
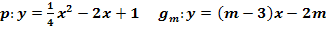
Lösung:
Diese Aufgabe hört sich schwierig an! Aber keine Angst, so schlimm ist sie gar nicht. Solltest du mit dem Begriff „Geradenschar“ nichts anfangen können, hier eine kurze Erklärung:
Eine Geradenschar bzw. eine Schar von Geraden bedeutet nichts anderes als viele Geraden gemeinsam. (Vergleiche:Eine Schar von Kindern = viele Kinder zusammen) Eine Funktionenschar erkennt man daran, dass neben x und y ein weiterer Buchstabe, in unseren Fall m, in der Funktionsgleichung auftaucht. Diesen zusätzlichen Buchstaben nennt man Scharparameter oder kurz Parameter, im Gegensatz zu x und y, die als Variablen bezeichnet werden. Der Scharparameter, hier m, ist immer eine festgelegte Zahl, also eine Konstante. Man kennt ihn zwar (noch) nicht, aber trotzdem steht m immer für eine konkrete Zahl. Das mag verwirrend erscheinen, da wir für m dennoch verschiedene Werte einsetzen können. Je nach dem, was für m eingesetzt wird, ergeben sich dann die unterschiedliche Geraden der Schar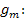 
y =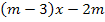 
.
Setzt man beispielsweise m = 2, erhält man die Gerade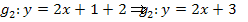 
Oder man wählt m = 3, so erhält man die Gerade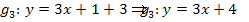 
Indem man also für m konkrete Zahlen einsetzt, bekommt man die verschiedenen Schargeraden. Diese Geraden haben natürlich alle jeweils eine andere Lage zu der gegebenen Parabel 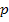. Unsere Aufgabe besteht nun darin, herauszufinden, für welches m sich eine Tangente, eine Sekante bzw. eine Passante ergibt.
