Lagebeziehungen zwischen Parabel und Gerade
Da die Geradengleichung einfacher ist, setzen wir in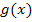 
ein.
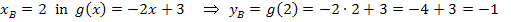
Der gesuchte Berührpunkt B lautet daher B(2|-1).
2. Bsp.:
Berechne die Koordinaten der Schnittpunkte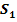 
und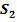 
der Geraden 
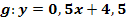mit der Parabel 
!
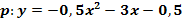Lösung:
Aus der Aufgabenstellung geht bereits hervor, dass die beiden Funktionen zwei Schnittpunkte haben. Um die x-Koordinaten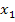 
und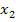 
dieser Schnittpunkte zu berechnen, setzen wir die beiden Funktionen gleich, stellen nach Null um und wenden die Mitternachtsformel an. In dieser Aufgabe muss nicht zuerst die Diskriminante D berechnet werden, da ja bereits klar ist, dass die Diskriminante positiv sein wird;sonst würden sich nicht zwei Schnittpunkte ergeben.
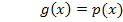
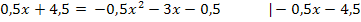
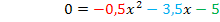
Zur Erinnerung: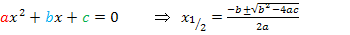 
(Mitternachtsformel)
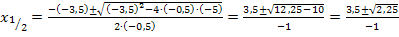
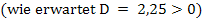
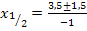
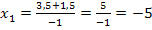
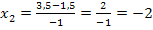
Nun müssen wir nur noch die entsprechenden y-Koordinaten der Schnittpunkte berechnen. Dazu setzen wir die soeben ermittelten x-Koordinaten in die Geradengleichung ein, genauer gesagt, wird einmal 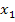und einmal 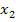für x in die Geradengleichung eingesetzt. (Man hätte natürlich auch in die Parabelgleichung einsetzen können, da die Schnittpunkte schließlich sowohl auf der Gerade 
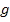als auch auf der Parabel 
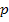liegen. Das Einsetzen in die Parabel ist aber umständlicher. Warum sollten wir das also machen?)
Hier noch einmal die Gleichung von :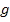
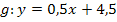
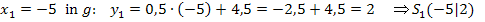
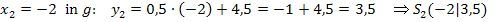
3. Bsp.:
Zeige durch Rechnung, dass die Gerade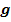 
und die Parabel 
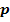keinen gemeinsamen Punkt besitzen!
Lösung:
Um zu beweisen, dass die Gerade 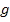und die Parabel 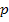keinen gemeinsamen Punkt besitzen, müssen wir die beiden Funktionsgleichungen gleichsetzen und zeigen, dass die Diskriminante D einen negativen Wert annimmt. Nur dann ergibt sich keine Lösung, also kein gemeinsamer Punkt der beiden Funktionen. Damit wir die Funktionen gleichsetzen können, müssen jedoch beide Funktionsgleichungen nach y aufgelöst vorliegen. Das ist bei der Gerade noch nicht der Fall. Deshalb stellen wir die Geradengleichung zuerst nach y um.
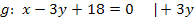
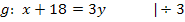
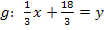
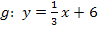
Jetzt könnten wir die Gerade mit der Parabel gleichsetzen. Da die Parabel jedoch in ihrer Scheitelform vorliegt, ist es praktischer, sie vorher noch auf die Form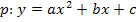 
zu bringen.
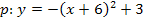
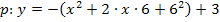
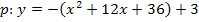
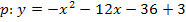
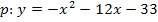
Nun setzen wir endlich die Gerade und die Parabel gleich.
