Lagebeziehungen zwischen Parabel und Gerade

Hinweis:

Enthält die Gleichung, die durch das Gleichsetzen der Gerade mit der Parabel entsteht, nur , aber kein x ohne Exponent, wird die Mitternachtsformel nicht angewendet, da die Gleichung dann viel einfacher zu lösen ist, indem man isoliert und falls möglich die Wurzel zieht. Vorsicht:Aus negativen Zahlen kann die Wurzel nicht gezogen werden;dann gibt es keine Lösung, also keine Schnittpunkte. Bei positiven Zahlen darf das 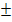vor der Wurzel nicht vergessen werden, sonst verliert man eine der beiden Lösungen! Näheres dazu im Kapitel Quadratische Gleichungen.

Damit das Ganze nicht nur graue Theorie bleibt, schauen wir uns doch gleich einmal einige typische Aufgabenbeispiele zum Thema Lagebeziehungen zwischen Parabel und Gerade an.

1. Bsp.:

Zeige, dass die Gerade 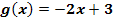Tangente an die Parabel 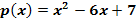ist! Berechne auch die Koordinaten des Berührpunkts B!

Lösung:

Wie oben schon erklärt, müssen zuerst die Funktionsgleichungen der Gerade und der Parabel gleichgesetzt werden.

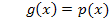
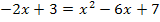
Dadurch ist eine gemischtquadratische Gleichung (Gleichung mit und x) entstanden. Wir wollen sie mit der Mitternachtsformel nach x auflösen. Da sich die Mitternachtsformel aber nur auf Gleichungen des Typs 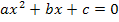anwenden lässt, müssen wir unsere Gleichung noch nach Null umstellen, d.h. alles auf eine Seite der Gleichung bringen, bevor wir die Mitternachtsformel anwenden können.

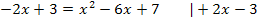
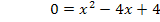
Da in dieser Aufgabe gezeigt werden soll, dass die Gerade Tangente an die Parabel ist, verwenden wir nicht sofort die ganze Mitternachtsformel. Es ist geschickter zuerst nur die Diskriminante zu berechnen. Da eine Tangente mit der Parabel nur einen gemeinsamen Punkt besitzt, muss unsere Gleichung genau eine Lösung haben, d.h. für die Diskriminante D = 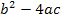muss gelten:D = 0

Wir müssen deshalb nun selbst D berechnen und es muss dabei Null herauskommen.

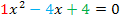
a b c

D =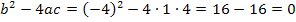

D = 0 Tangente

Dadurch ist gezeigt, dass die Gerade Tangente ist. Um außerdem die Koordinaten des Berührpunktes B zu erhalten, setzen wir nun in die komplette Mitternachtsformel ein. Beachte, dass D schon berechnet ist. Man braucht also für die Diskriminante nur D = 0 einzusetzen und nicht noch einmal komplett neu zurechnen. Durch das Einsetzen in die Mitternachtsformel erhalten wir die x-Koordinate des Berührpunktes B.

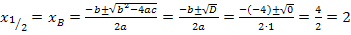
Nun fehlt noch die y-Koordinate von B. Wir erhalten sie durch Einsetzen der soeben berechneten x-Koordinate von B in eine der beiden Funktionsgleichungen 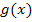oder .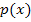

---