Lagebeziehungen zwischen Parabel und Gerade
Damit die „Mitternachtsformel“ angewendet werden kann, muss die Gleichung aber zuerst auf die Form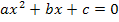 
gebracht werden. Das bedeutet, dass die durch das Gleichsetzen der beiden Funktionen p(x) und g(x) entstandene gemischtquadratische Gleichung so umgeformt werden muss, dass auf einer Seite der Gleichung eine Null zu stehen kommt. Man bringt also alles auf eine Seite der Gleichung. Ob man alles auf die linke oder alles auf die rechte Seite bringt, ist egal. Nun kann in die Mitternachtsformel eingesetzt werden.
Zur Erinnerung:
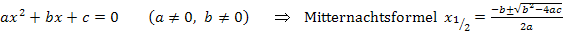
Der Ausdruck unter der Wurzel wird Diskriminante D genannt.
D =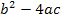 
Die Diskriminante D ist entscheidend für die Anzahl der Lösungen und gibt daher Aufschluss über die Lage von Parabel und Gerade zueinander:
Bekanntlich kann aus einer negativen Zahl keine Wurzel gezogen werden. Daher gibt es keine Lösung, also keine Schnittpunkte von Parabel p und Gerade g, wenn die Diskriminante D einen negativen Wert ergibt.
Ist D dagegen positiv, kann die Wurzel (zumindest näherungsweise) gezogen werden. Es ergeben sich wegen des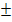 
vor der Wurzel im Zähler der Mitternachtsformel zwei verschiedene Lösungen für 
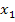und 
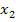. Es existieren daher zwei verschiedene Schnittpunkte von Parabel und Gerade, wenn die Diskriminante D positiv ist. Die soeben berechneten Werte 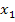und 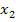sind die x-Koordinaten der beiden Schnittpunkte. Um die jeweiligen y-Koordinaten der Schnittpunkte zu erhalten, setzt man einmal 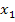und einmal 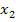entweder in die Funktionsgleichung der Parabel p oder in die Gleichung der Gerade g für x ein. Einfacher ist es natürlich in die Geradengleichung einzusetzen.
Ergibt sich für die Diskriminante D der Wert Null, gibt es genau eine Lösung, also einen Berührpunkt von Parabel und Gerade, da sich dann für 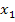und 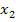der selbe Wert ergibt. (Ob man 
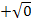oder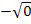 
rechnet, ist schließlich egal, es kommt das gleiche Ergebnis heraus.) Die Gerade ist daher Tangente an die Parabel, wenn die Diskriminante D gleich Null ist. Der soeben berechnete Wert 
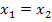ist die x-Koordinate des Berührpunktes B und wird oft mit 
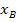bezeichnet. Der Berührpunkt liegt natürlich gleichzeitig auf beiden Funktionen. Daher kann die x-Koordinate 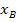entweder in die Funktionsgleichung der Parabel p oder in die Gleichung der Gerade g für x eingesetzt werden, um die y-Koordinate des Berührpunktes zu berechnen. Einfacher ist es natürlich 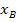in die Geradengleichung einzusetzen.
| Zusammenfassung:
Überprüfung der Lagebeziehungen einer Parabel p(x) und einer Gerade g(x) · Parabel und Gerade gleichsetzen: p(x) = g(x) · Gleichung nach Null auflösen: · Mitternachtsformel anwenden: · Diskriminante D = D D = D · eventuell y-Koordinate(n) der Schnittpunkte bzw. des Berührpunktes berechnen, indem die berechnete(n) x-Koordinate(n) in g(x) eingesetzt werden. |
)
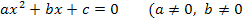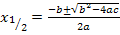
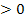⇔ 2 Schnittpunkte
(g ist Sekante von p)
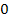⇔ 1 Berührpunkt
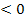⇔ kein gemeinsamer Punkt (g ist Passante von p)
