Symmetrieachse und zwei weitere Informationen gegeben
Der Schnittpunkt mit der y-Achse lautet also (0|6). Wir setzen die Koordinaten dieses Punktes für x und y in Gleichung* ein:
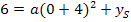
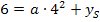

Die beiden Gleichungen I und II bilden zusammen ein Gleichungssystem mit zwei Gleichungen und zwei Unbekannten. Es kann entweder mit dem Gleichsetzungs-, dem Einsetzungs- oder dem Additionsverfahren gelöst werden. Da die meisten Schüler das Einsetzungsverfahren bevorzugen und es hier relativ praktisch ist, wird im Folgenden dieses Verfahren vorgeführt.
Hier noch einmal zur besseren Übersicht das zu lösende Gleichungssystem:
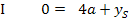
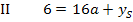
Wir lösen nun eine der beiden Gleichungen nach a oder 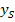 auf und setzen dies in die andere Gleichung ein. Hier lässt sich natürlich leichter nach
auf und setzen dies in die andere Gleichung ein. Hier lässt sich natürlich leichter nach 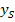 als nach a auflösen. Welche der beiden Gleichungen nach
als nach a auflösen. Welche der beiden Gleichungen nach 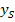 aufgelöst wird, ist an sich egal;es geht hier schließlich in beiden Gleichungen ganz leicht. Wir entscheiden uns dafür, Gleichung I nach
aufgelöst wird, ist an sich egal;es geht hier schließlich in beiden Gleichungen ganz leicht. Wir entscheiden uns dafür, Gleichung I nach 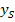 aufzulösen. Danach wird dann in Gleichung II eingesetzt.
aufzulösen. Danach wird dann in Gleichung II eingesetzt.
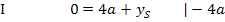
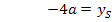
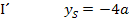
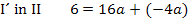
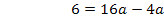
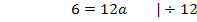
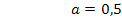
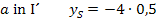
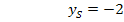
Nun sind beide Unbekannten berechnet: 
Sie müssen nur noch in Gleichung* (von ganz oben) eingesetzt werden. Dann ist die Parabel in Scheitelform aufgestellt:
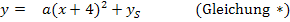
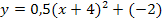
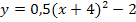
- Page 3 of 3
- « Previous
- 1
- 2
- 3
- Next »

