Symmetrieachse und zwei weitere Informationen gegeben

Die allgemeine Gleichung der Symmetrieachse lautet daher: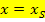

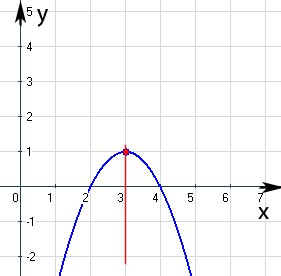
Abb. Graph der Funktion 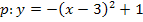mit Symmetrieachse x = 3

Nun dürfte es verständlich sein, warum die Angabe der Symmetrieachse gleichbedeutend mit der Angabe der x-Koordinate des Scheitels 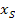ist.

Nun folgen zwei Beispiele, wie mit der Gleichung der Symmetrieachse und zwei weiteren Informationen, z.B. dem Öffnungsfaktor a und einem Kurvenpunkt oder zwei Kurvenpunkten, die Gleichung einer Parabel ermittelt werden kann.

1. Bsp.:

Ermittle die Gleichung einer nach unten geöffneten Normalparabel, welche durch den Punkt P(-1|-2) verläuft und die Symmetrieachse x = 1,5 besitzt! Gib die Funktion in der Form 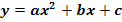an!

Lösung:

Da es sich um eine nach unten geöffnete Normalparabel handelt, wissen wir, dass für den Öffnungsfaktor a gilt: a = -1

Die Symmetrieachse hat die Gleichung x = 1,5. Daher muss der Scheitel die x-Koordinate 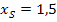haben muss.

Wir setzen diese Angaben in die Scheitelform 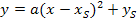ein:

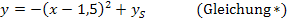
Die y-Koordinate des Scheitels 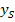ist momentan noch unbekannt. wir können sie jedoch leicht berechnen, wenn wir nun auch die Koordinaten des angegebenen Kurvenpunkts P(-1|-2) für x und y einsetzen.

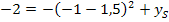
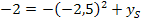
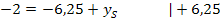
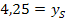
Nun müssen wir nur noch den soeben berechneten Wert für 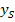in Gleichung* einsetzen und in die Form 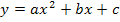umrechnen.

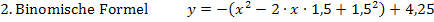
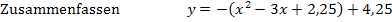
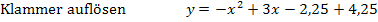
2. Bsp.: Von einer Parabel ist bekannt, dass sie die x-Achse bei 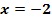und die y-Achse bei 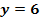schneidet. Die Symmetrieachse der Parabel hat die Gleichung 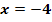. Ermittle die Gleichung der Parabel in Scheitelform!

Lösung:

In der Aufgabenstellung ist die Symmetrieachse 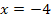gegeben. Daher kennt man die x-Koordinate des Scheitels:

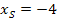
Wir setzen diese Angabe in die Scheitelform 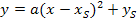ein:

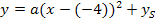
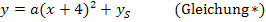
Außerdem ist angegeben, dass die Parabel die x-Achse bei 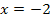schneidet. Jeder Punkt, der auf der x-Achse liegt, hat die y-Koordinate y = 0 (Gleichung der x-Achse). Daher wissen wir, dass der Punkt (-2|0) auf der Parabel liegt. Wir setzen ihn für x bzw. y in Gleichung* ein:

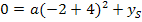
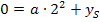
Da Gleichung I zwei Unbekannte enthält, kann im Moment weder a noch 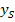direkt berechnet werden. Wir benötigen noch eine zweite Gleichung, welche diese Unbekannten enthält. Zu dieser Gleichung kommt man folgender maßen:

Es ist bekannt, dass die Parabel die y-Achse bei 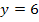schneidet. Jeder Punkt der y-Achse hat die x-Koordinate x = 0 (Gleichung der y-Achse).

---