Normalparabel (nach oben oder unten geöffnet) und zwei Kurvenpunkte gegeben
) Auf jeden Fall steht in beiden Gleichungen vor c das Gleiche. Daher fällt c weg, wenn man die Gleichungen I und II voneinander abzieht.
Wichtig:Die komplette linke Seite der einen Gleichung muss von der kompletten linken Seite der anderen Gleichung abgezogen werden und gleichzeitig die komplette rechte Seite der einen von der kompletten rechten Seite der anderen Gleichung.
Welche Gleichung von welcher subtrahiert wird ist egal;c fällt dabei immer heraus. Es entsteht durch die Subtraktion I – II bzw. II – I somit eine Gleichung, die nur noch b als Unbekannte enthält, so dass man b leicht durch Umstellen berechnen kann.
Anmerkung:Dieses Verfahren heißt zwar „Additionsverfahren“, die Subtraktion beider Gleichungen ist dennoch erlaubt, da z.B. die Subtraktion II – I der Addition 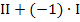 entspricht. Genaueres dazu findest du im Kapitel Additionsverfahren.
entspricht. Genaueres dazu findest du im Kapitel Additionsverfahren.
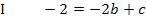
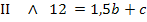
Hier empfiehlt es sich I von II abzuziehen, weil sich dadurch positive Zahlen ergeben. Der folgende Zwischenschritt (oberste Zeile der folgenden Rechnung) muss von dir, wenn du selbst rechnest, nicht aufgeschrieben werden;er ist nur zur Verdeutlichung des Verfahrens gezeigt. Erst die darauf folgende Zeile musst du auf jeden Fall wieder hinschreiben.
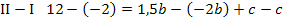
![]()
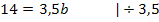
![]()
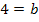
Um c zu ermitteln, wird nun der soeben berechnete Wert für b in Gleichung I oder II eingesetzt. Wie schon beim Einsetzungsverfahren erläutert, setzt man in diesem Beispiel am besten in I ein.
b = 4 in I eingesetzt: 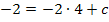
![]()
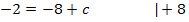
![]()
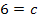
Im Vergleich zum Einsetzungsverfahren führt das Additionsverfahren hier offensichtlich wesentlich schneller zu den gesuchten Lösungen.
Jetzt sind wir fast fertig. Wir wissen nun: b = 4 ; c = 6
Man muss diese Werte nur noch für b und c in den allgemeinen Ansatz der nach unten geöffneten Normalparabel 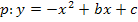 einsetzten.
einsetzten.
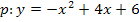
| Zusammenfassung:
Gesucht: Nach oben bzw. unten geöffnete Normalparabel durch die Punkte A und B · Nach oben geöffnete Normalparabel: · Nach unten geöffnete Normalparabel: · Koordinaten der Kurvenpunkte A und B einsetzen:
· Gleichungssystem mit dem Einsetzungs- oder Additionsverfahren lösen: Berechnete Werte für b und c in den allgemeinen Ansatz der Parabel |
- Page 4 of 4
- « Previous
- 1
- 2
- 3
- 4
- Next »

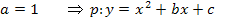
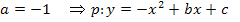
 Zwei Gleichungen I und II für die beiden Unbekannten b und c (Gleichungssystem)
Zwei Gleichungen I und II für die beiden Unbekannten b und c (Gleichungssystem)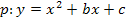 bzw.
bzw. 