Normalparabel (nach oben oder unten geöffnet) und zwei Kurvenpunkte gegeben
Beispiel:Ermittle die Gleichung einer nach unten geöffneten Normalparabel, die durch die Punkte A(-2|-6) und B(1,5|9,75) verläuft!
Lösung:
Es soll die Funktionsgleichung einer nach unten geöffneten Normalparabel ermittelt werden. Daher ist a = -1 und es gilt der allgemeine Ansatz:
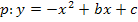
Nun setzen wir nacheinander die Koordinaten der beiden Punkte für x und y ein.
A(-2|-6) einsetzen:
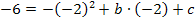
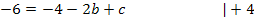
Gleichung I: 
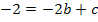
B(1,5|9,75) einsetzen: 
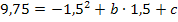
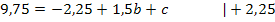
Gleichung II: 
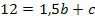
Die beiden Gleichungen I und II werden als Gleichungssystem, d.h. untereinander und mit dem Zeichen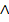 
vor II geschrieben:
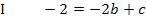
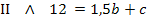
Das Gleichungssystem (2 Gleichungen für die 2 Unbekannten b und c) kann entweder mit dem Einsetzungsverfahren oder mit dem Additionsverfahren gelöst werden. Du kannst selbst wählen, welches Verfahren dir leichter fällt. Im Folgenden werden hier ausnahmsweise beide Verfahren vorgeführt, damit du sehen kannst, wie sie jeweils funktionieren. Du brauchst, wie gesagt, nur eines der beiden, im Folgenden gezeigten Verfahren beherrschen.
1. Methode:Einsetzungsverfahren
Es wird eine der beiden Gleichungen nach einer der beiden Unbekannten, also nach b oder c, aufgelöst. Hier bietet es sich an nach c aufzulösen, da vor c in den Gleichungen keine Zahl steht. Welche der beiden Gleichungen nach c umgestellt wird, ist egal. Hier lassen sich schließlich beide Gleichungen leicht nach c auflösen, weil bei beiden keine Zahl vor c steht. Wir entscheiden uns beispielsweise für Gleichung I.
Hier noch einmal die beiden Gleichungen:
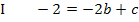
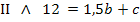
I nach c auflösen: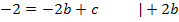 
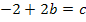
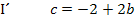
Dieser Ausdruck wird nun in die andere Gleichung (hier II) für c eingesetzt und dann nach b aufgelöst:
I` in II eingesetzt: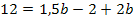 
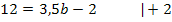
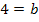
Die erste Unbekannte haben wir nun berechnet:b = 4
Diesen Wert setzt man jetzt in Gleichung I oder II ein, um die zweite Unbekannte c zu ermitteln. Da in diesem Beispiel in Gleichung I die „schöneren“ Zahlen vorkommen, setzen wir b in I ein. (Einsetzen von b in II führt natürlich zum selben Ergebnis für c, doch enthält II Dezimalbrüche, also Kommazahlen, und wer rechnet denn lieber mit solchen Zahlen!)
b = 4 in I eingesetzt: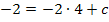 
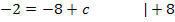
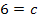
2. Methode:Additionsverfahren
Das Additionsverfahren ist hier besonders einfach, da sowohl in Gleichung I als auch in Gleichung II vor der Unbekannten c keine Zahl steht. (Genau genommen ist c natürlich das Selbe wie 1c, also steht eigentlich vor c jeweils die Zahl 1!
